
在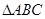 中,
中,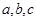 分别为内角
分别为内角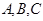 所对的边,且满足
所对的边,且满足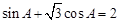 .
.
(Ⅰ)求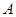 的大小;
的大小;
(Ⅱ)现给出三个条件:①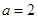 ; ②
; ②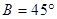 ;③
;③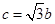 .
.
试从中选出两个可以确定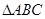 的条件,写出你的选择并以此为依据求
的条件,写出你的选择并以此为依据求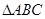 的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分)
的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分)
科目:高中数学 来源: 题型:
在![]() 中,
中,![]() 分别为内角
分别为内角![]() 所对的边,且满足
所对的边,且满足![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)现给出三个条件:①![]() ; ②
; ②![]() ;③
;③![]() .
.
试从中选出两个可以确定![]() 的条件,写出你的选择并以此为依据求
的条件,写出你的选择并以此为依据求![]() 的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)
的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)
查看答案和解析>>
科目:高中数学 来源:2014届陕西省高二上学期期末考试理科数学试卷(解析版) 题型:填空题
在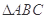 中,
中,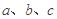 分别为内角
分别为内角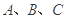 所对的边,且
所对的边,且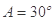 .现给出三个条件:①
.现给出三个条件:①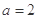 ; ②
; ②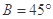 ;③
;③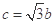 .试从中选出两个可以确定
.试从中选出两个可以确定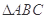 的条件,并以此为依据求
的条件,并以此为依据求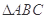 的面积.(只需写出一个选定方案即可)你选择的条件是 (用序号填写);由此得到的
的面积.(只需写出一个选定方案即可)你选择的条件是 (用序号填写);由此得到的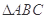 的面积为 .
的面积为 .
查看答案和解析>>
科目:高中数学 来源:汕头市2009-2010学年度第二学期高三级数学综合测练题(理二) 题型:填空题
在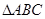 中,
中, 分别为内角
分别为内角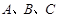 所对的边,且
所对的边,且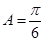 .现给出三个条件:①
.现给出三个条件:①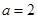 ; ②
; ②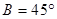 ;③
;③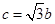 .试从中选出两个可以确定
.试从中选出两个可以确定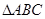 的条件,并以此为依据求
的条件,并以此为依据求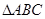 的面积.(只需写出一个选定方案即可)你选择的条件是
(用序号填写);由此得到的
的面积.(只需写出一个选定方案即可)你选择的条件是
(用序号填写);由此得到的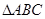 的面积为 .
的面积为 .
查看答案和解析>>
科目:高中数学 来源:2011届广东省高三高考全真模拟试卷数学理卷二 题型:填空题
..在 中,
中, 分别为内角
分别为内角 所对的边,且
所对的边,且 .
.
现给出三个条件:① ; ②
; ②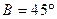 ;③
;③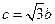 .试从中选出两个可以确定
.试从中选出两个可以确定 的条件,并以此为依据求
的条件,并以此为依据求 的面积.(只需写出一个选定方案即可)你选择的条件是 (用序号填写);由此得到的
的面积.(只需写出一个选定方案即可)你选择的条件是 (用序号填写);由此得到的 的面积为
的面积为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com