
【题目】如图所示,四棱锥![]() 中,底面
中,底面![]() 为菱形,且直线
为菱形,且直线![]() 又棱
又棱![]()
![]() 为
为![]() 的中点,
的中点, ![]()
(Ⅰ) 求证:直线![]() ;
;
(Ⅱ) 求直线![]() 与平面
与平面![]() 的正切值.
的正切值.

【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由线面垂直的判定定理证明,EA⊥AB,EA⊥PA,得EA⊥平面PAB;(2)∠AEP为直线AE与平面PCD所成角,所以![]() 。
。
试题解析:
解:(1)证明:∵∠ADE=∠ABC=60°,ED=1,AD=2
∴△AED是以∠AED为直角的Rt△
又∵AB∥CD, ∴EA⊥AB
又PA⊥平面ABCD,∴EA⊥PA,
∴EA⊥平面PAB,
(2)
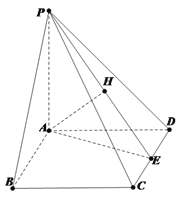
如图所示,连结PE,过A点作AH⊥PE于H点
∵CD⊥EA, CD⊥PA
∴CD⊥平面PAE,∴AH⊥CD,又AH⊥PE
∴AH⊥平面PCD
∴∠AEP为直线AE与平面PCD所成角
在Rt△PAE中,∵PA=2,AE=![]()
∴![]()


科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,角A,B,C所对的边分别为a,b,c,( ![]() a﹣sinC)cosB=sinBcosC,b=4
a﹣sinC)cosB=sinBcosC,b=4 ![]() .
. 
(1)求角B的大小;
(2)D为BC边上一点,若AD=2,S△DAC=2 ![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣5:不等式选讲
已知函数f(x)=|x﹣2|﹣|x﹣5|.
(1)证明:﹣3≤f(x)≤3;
(2)求不等式f(x)≥x2﹣8x+15的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个几何体的平面展开图,其中四边形ABCD为正方形,△PDC, △PBC, △PAB, △PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为 ( )

A. 平面BCD⊥平面PAD B. 直线BE与直线AF是异面直线
C. 直线BE与直线CF共面 D. 面PAD与面PBC的交线与BC平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]()
![]() 有相同的焦点.
有相同的焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,问:以线段
,问:以线段![]() 为直径的圆是否经过一定点
为直径的圆是否经过一定点![]() ?若存在,求出定点
?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖南省某自来水公司每个月(记为一个收费周期)对用户收一次水费,收费标准如下:当每户用水量不超过30吨时,按每吨2元收取;当该用户用水量超过30吨但不超过50吨时,超出部分按每吨3元收取;当该用户用水量超过50吨时,超出部分按每吨4元收取。
(1)记某用户在一个收费周期的用水量为![]() 吨,所缴水费为
吨,所缴水费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)在某一个收费周期内,若甲、乙两用户所缴水费的和为214元,且甲、乙两用户用水量之比为3:2,试求出甲、乙两用户在该收费周期内各自的用水量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10 ![]() 米,记∠BHE=θ.
米,记∠BHE=θ. 
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)问:当θ取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com