
【题目】已知函数![]()
(1) 若![]() ,求
,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若![]() 在定义域上是单调函数,求
在定义域上是单调函数,求![]() 的取值范围;
的取值范围;
(3)若![]() 存在两个极值点
存在两个极值点![]() ,求证:
,求证: ![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() ,其导函数为
,其导函数为![]() ,若对任意的实数
,若对任意的实数![]() ,都有
,都有![]() 恒成立,则使
恒成立,则使![]() 成立的实数
成立的实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B. (﹣∞,﹣1)∪(1,+∞)
B. (﹣∞,﹣1)∪(1,+∞)
C. (﹣1,1) D. (﹣1,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位网民在网上光顾某网店,经过一番浏览后,对该店铺中的A,B,C三种商品有购买意向.已知该网民购买A种商品的概率为 ![]() ,购买B种商品的槪率为
,购买B种商品的槪率为 ![]() ,购买C种商品的概率为
,购买C种商品的概率为 ![]() .假设该网民是否购买这三种商品相互独立
.假设该网民是否购买这三种商品相互独立
(1)求该网民至少购买2种商品的概率;
(2)用随机变量η表示该网民购买商品的种数,求η的槪率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数:①f(x)=3|x| , ②f(x)=x3 , ③f(x)=ln ![]() ,④f(x)=
,④f(x)= ![]() ,⑤f(x)=﹣x2+1中,既是偶函数,又是在区间(0,+∞)上单调递减函数为 . (写出符合要求的所有函数的序号).
,⑤f(x)=﹣x2+1中,既是偶函数,又是在区间(0,+∞)上单调递减函数为 . (写出符合要求的所有函数的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设有正整数![]() ,使得
,使得![]() 成等差数列,求
成等差数列,求![]() 的值;
的值;
(3)设![]() ,对于给定的
,对于给定的![]() ,求三个数
,求三个数![]() 经适当排序后能构成等差数列的充要条件.
经适当排序后能构成等差数列的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证: 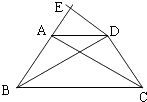
(1)△ABC≌△DCB;
(2)DEDC=AEBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() 元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比例 |
|
|
|
|
|
该公司从注册的会员中, 随机抽取了![]() 位进行统计, 得到统计数据如下:
位进行统计, 得到统计数据如下:
消费次第 | 第 | 第 | 第 | 第 | 第 |
频数 |
|
|
|
|
|
假设汽车美容一次, 公司成本为![]() 元, 根据所给数据, 解答下列问题:
元, 根据所给数据, 解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次, 求这两次消费中, 公司获得的平均利润;
(3)以事件发生的频率作为相应事件发生的概率, 设该公司为一位会员服务的平均利润为![]() 元, 求
元, 求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com