
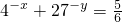 ,
,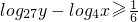 ,27y-4x≤1,则x+y的取值范围是________.
,27y-4x≤1,则x+y的取值范围是________.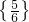
 ,y=
,y= 时该等式成立,同时把相应的x和y的值代入后面的两个不等式等号也成立,把给出的等式的左边变负指数幂为正指数幂,分析x和y的变化规律,知道y随x的增大而减小,而当x增大y减小时,两不等式不成立,因此断定,同时满足等式和不等式的x,y取值唯一,从而可得x+y的取值范围.
时该等式成立,同时把相应的x和y的值代入后面的两个不等式等号也成立,把给出的等式的左边变负指数幂为正指数幂,分析x和y的变化规律,知道y随x的增大而减小,而当x增大y减小时,两不等式不成立,因此断定,同时满足等式和不等式的x,y取值唯一,从而可得x+y的取值范围. ,y=
,y= 时,
时,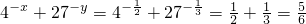 ,
,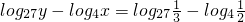 =
=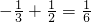 ,
,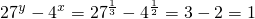 .
. 知,等式右边一定,左边y随x的增大而减小,
知,等式右边一定,左边y随x的增大而减小, ,
, ,y=
,y= 时,条件成立,
时,条件成立, }.
}. }.
}.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com