
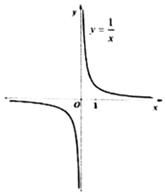
 阅读下面材料,尝试类比探究函数y=x2-$\frac{1}{{x}^{2}}$的图象,写出图象特征,并根据你得到的结论,尝试猜测作出函数对应的图象.
阅读下面材料,尝试类比探究函数y=x2-$\frac{1}{{x}^{2}}$的图象,写出图象特征,并根据你得到的结论,尝试猜测作出函数对应的图象.分析 通过函数的定义域,函数与x的交点情况,y值的变化趋势,函数的奇偶性和函数的单调性,归纳函数的性质即可.
解答 解:(1)在y=x2-$\frac{1}{{x}^{2}}$中,x≠0,可以推测出:对应的图象不经过y轴,即与y轴不相交,
(2)令y=0,即x2-$\frac{1}{{x}^{2}}$=0,解得x=±1,可以推测出,对应的图象与x相交,交点坐标为(1,0)和(-1,0),
(3)在y=x2-$\frac{1}{{x}^{2}}$中,当0<x<1时,$\frac{1}{{x}^{2}}$>1>x2,则y<0,当x>1时,$\frac{1}{{x}^{2}}$<1<x2,则y>0,可以推测出:对应的图象在区间(0,1)上图象在x轴的下方,在区间(1,+∞)上图象在x轴的上方,
(4)在y=x2-$\frac{1}{{x}^{2}}$中,若x∈(0,+∞),则
当x逐渐增大时$\frac{1}{{x}^{2}}$逐渐减小,x2-$\frac{1}{{x}^{2}}$,逐渐增大,即y逐渐增大,所以原函数在(0,+∞)是增函数,
可以推测出:对应的图象越向右逐渐升高,是单调递增的趋势,
(5)由函数y=x2-$\frac{1}{{x}^{2}}$可知f(-x)=f(x),即函数为偶函数,可以推测出:对应的图象关于y轴对称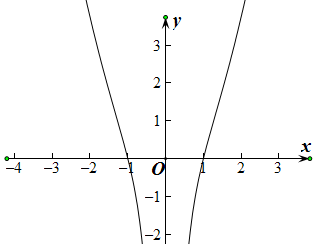
点评 本题考查了类比推理的问题,关键是掌握函数的性质,以及题目所告诉的例子,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
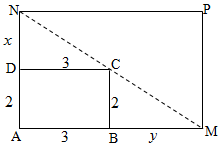 如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值.
如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,7) | B. | (7,7) | C. | (7,1) | D. | (3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{7}{5}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}=2\overrightarrow{AE}$ | B. | $\overrightarrow{AD}=4\overrightarrow{AE}$ | C. | $\overrightarrow{AD}=2\overrightarrow{EA}$ | D. | $\overrightarrow{AD}=4\overrightarrow{EA}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com