
设等差数列 的前
的前 项和为
项和为 .在同一个坐标系中,
.在同一个坐标系中,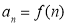 及
及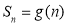 的部分图象如图所示,则( )
的部分图象如图所示,则( )

(A)当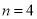 时,
时, 取得最大值
取得最大值
(B)当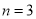 时,
时, 取得最大值
取得最大值
(C)当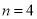 时,
时, 取得最小值
取得最小值
(D)当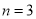 时,
时, 取得最小值
取得最小值
A
【解析】
试题分析:首先分析图象中三个点各自的含义,若横坐标为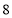 的点表示
的点表示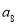 ,那么
,那么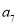 的情况分为两种:(1)
的情况分为两种:(1)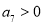 ,在这种情况下,根据图象可知,
,在这种情况下,根据图象可知,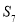 必然小于
必然小于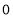 ,但我们可以根据图象发现,
,但我们可以根据图象发现,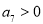 ,
,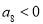 ,等差数列为单调递减的,说明数列从第一项至第七项应该都是大于
,等差数列为单调递减的,说明数列从第一项至第七项应该都是大于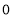 的,那么前7项和
的,那么前7项和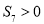 ,与图象给出的信息矛盾,故
,与图象给出的信息矛盾,故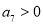 不成立;(2)
不成立;(2)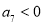 ,在这种情况下,根据图象可以推理出前7项和
,在这种情况下,根据图象可以推理出前7项和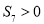 ,但是,
,但是, ,说明数列单调递增,且从第一项至第八项均小于
,说明数列单调递增,且从第一项至第八项均小于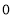 ,那么前7项和必然大于
,那么前7项和必然大于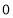 ,又产生矛盾。说明横坐标为
,又产生矛盾。说明横坐标为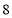 处的点表示的是数列的前8项和
处的点表示的是数列的前8项和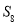 ,此时需要分析横坐标为
,此时需要分析横坐标为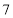 处的两个点各自的含义,若
处的两个点各自的含义,若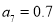 ,则
,则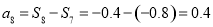 ,说明数列单调递减,那么可知数列在第一项至第8项均为正数,那么
,说明数列单调递减,那么可知数列在第一项至第8项均为正数,那么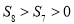 ,与图象信息矛盾,故
,与图象信息矛盾,故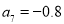 ,
,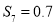 ,
,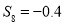 ,可以解得
,可以解得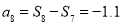 ,可知等差数列公差为
,可知等差数列公差为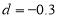 ,接下来可以有两种基本思路去处理.
,接下来可以有两种基本思路去处理.
方法一:直接求解数列通项,根据公差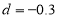 ,解得
,解得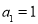 ,那么可以解得前
,那么可以解得前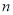 项和的表达式为
项和的表达式为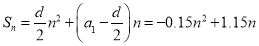 ,可知其对称轴
,可知其对称轴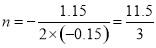 ,距它最近的整数为
,距它最近的整数为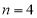 ,故其在
,故其在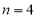 时取最大值,故选A.
时取最大值,故选A.
方法二:从前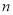 项和的最值性质可以看出,数列本身正负发生改变的地方是产生最值的地方,根据分析可知,
项和的最值性质可以看出,数列本身正负发生改变的地方是产生最值的地方,根据分析可知,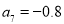 ,那么
,那么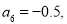
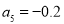 ,
, ,可见,数列从第一项至第四项均是正数,此时前
,可见,数列从第一项至第四项均是正数,此时前 项和越加越大,最大值在第四项取到,故选A.
项和越加越大,最大值在第四项取到,故选A.
考点:等差数列及其前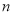 项和性质.
项和性质.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:填空题
在区间[0,3]上任取一个数m,则函数f(x)=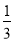 x3-x2+mx是R上的单调函数的概率是_____________.
x3-x2+mx是R上的单调函数的概率是_____________.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试文科数学试卷(解析版) 题型:解答题
已知数列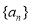 是公差大于零的等差数列,数列
是公差大于零的等差数列,数列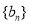 为等比数列,且
为等比数列,且 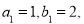
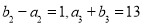
(1)求数列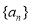 和
和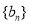 的通项公式
的通项公式
(2)设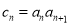 ,求数列
,求数列 前n项和
前n项和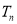 .
.
查看答案和解析>>
科目:高中数学 来源:2015届北京市海淀区高三上学期期中练习文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数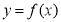 ,
,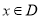 ,设曲线
,设曲线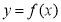 在点
在点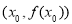 处的切线方程为
处的切线方程为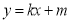 . 如果对任意的
. 如果对任意的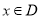 ,均有:
,均有:
①当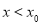 时,
时,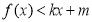 ;
;
②当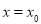 时,
时, ;
;
③当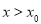 时,
时,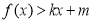 ,
,
则称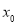 为函数
为函数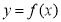 的一个“? -点”.
的一个“? -点”.
(1)判断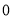 是否是下列函数的“? -点”:
是否是下列函数的“? -点”:
①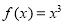 ; ②
; ②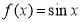 .(只需写出结论)
.(只需写出结论)
(2)设函数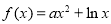 .
.
(ⅰ)若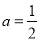 ,证明:
,证明: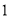 是函数
是函数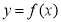 的一个“? -点”;
的一个“? -点”;
(ⅱ)若函数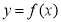 存在“? -点”,直接写出
存在“? -点”,直接写出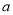 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届北京市海淀区高三上学期期中练习文科数学试卷(解析版) 题型:填空题
为净化水质,向一个游泳池加入某种化学药品,加药后池水中该药品的浓度 (单位:
(单位: )随时间
)随时间 (单位:
(单位: )的变化关系为
)的变化关系为 ,则经过_______
,则经过_______ 后池水中药品浓度达到最大.
后池水中药品浓度达到最大.
查看答案和解析>>
科目:高中数学 来源:2015届北京市朝阳区高三上学期期中统一考试理科数学试卷(解析版) 题型:解答题
(本小题满分13分)如图,在△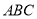 中,
中,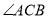 为钝角,
为钝角,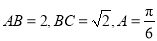 .
.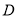 为
为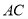 延长线上一点,且
延长线上一点,且 .
.

(Ⅰ)求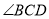 的大小;
的大小;
(Ⅱ)求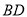 的长及△
的长及△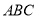 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试文科数学试卷(解析版) 题型:解答题
已知椭圆 经过点
经过点 ,且两焦点与短轴的两个端点的连线构成一正方形.
,且两焦点与短轴的两个端点的连线构成一正方形.
(1)求椭圆 的方程;
的方程;
(2)直线 与椭圆
与椭圆 交于
交于 ,
, 两点,若线段
两点,若线段 的垂直平分线经过点
的垂直平分线经过点 ,求
,求
( 为原点)面积的最大值.
为原点)面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com