
【题目】在数列{an},{bn}中,an=bn+n,bn=﹣an+1.
(1)证明:数列{an+3bn}是等差数列.
(2)求数列![]() 的前n项和Sn.
的前n项和Sn.
【答案】(1)证明见解析;(2)Sn![]()
【解析】
(1)可将bn=﹣an+1代入an=bn+n计算可得数列{an}的通项公式,然后根据bn=﹣an+1可得数列{bn}的通项公式,即可计算出数列{an+3bn}的通项公式,再根据等差数列的定义法可证明数列{an+3bn}是等差数列;
(2)先根据(1)的结果计算出数列![]() 的通项公式,然后根据通项公式的特点可采用错位相减法计算出前n项和Sn.
的通项公式,然后根据通项公式的特点可采用错位相减法计算出前n项和Sn.
(1)证明:由题意,将bn=﹣an+1代入an=bn+n,可得
an=bn+n=﹣an+1+n,即2an=n+1,
∴an![]() ,n∈N*,
,n∈N*,
∴bn=﹣an+1![]() 1
1![]() ,n∈N*,
,n∈N*,
∴an+3bn![]() 3
3![]() 2﹣n,
2﹣n,
∵(an+1+3bn+1)﹣(an+3bn)=2﹣(n+1)﹣(2﹣n)=﹣1,
∴数列{an+3bn}是以﹣1为公差的等差数列.
(2)由(1)知,![]() ,
,
则Sn![]() ,
,
∴![]() Sn
Sn![]() ,
,
两式相减,可得
![]() Sn
Sn![]()
![]() (
(![]() )
)![]()

![]() ,/span>
,/span>
∴Sn![]() .
.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关……”其大意为:“某人从距离关口三百七十八里处出发,第一天走得轻快有力,从第二天起,由于脚痛,每天走的路程为前一天的一半,共走了六天到达关口……” 那么该人第一天走的路程为______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到,任画一条线段,然后把它均分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了4条小线段构成的折线,称为“一次构造”;用同样的方法把每条小线段重复上述步骤,得到16条更小的线段构成的折线,称为“二次构造”,…,如此进行“![]() 次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取
次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取![]() ,
,![]() )
)

A.16B.17C.24D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为:
中,曲线C的参数方程为: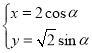 (
(![]() 为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程;
(Ⅱ)设点P的直角坐标为![]() ,若直线l与曲线C分别相交于A,B两点,求
,若直线l与曲线C分别相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学经典《数书九章》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”,将四个面都为直角三角形的四面体称之为“鳖臑”.在如图所示的阳马![]() 中,底面ABCD是矩形.
中,底面ABCD是矩形.![]() 平面
平面![]() ,
,![]() ,
,![]() ,以
,以![]() 的中点O为球心,AC为直径的球面交PD于M(异于点D),交PC于N(异于点C).
的中点O为球心,AC为直径的球面交PD于M(异于点D),交PC于N(异于点C).
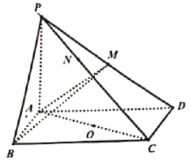
(1)证明:![]() 平面
平面![]() ,并判断四面体MCDA是否是鳖臑,若是,写出它每个面的直角(只需写出结论);若不是,请说明理由;
,并判断四面体MCDA是否是鳖臑,若是,写出它每个面的直角(只需写出结论);若不是,请说明理由;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实党中央对新冠肺炎疫情防控工作的部署和要求,坚决防范疫情向校园蔓延,切实保障广大师生身体健康和生命的安全,教育主管部门决定通过电视频道、网络平台等多种方式实施线上教育教学工作.某教育机构为了了解人们对其数学网课授课方式的满意度,从经济不发达的A城市和经济发达的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如下:
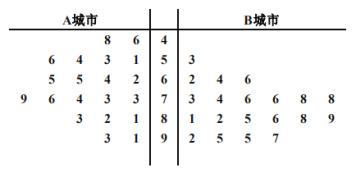
若评分不低于80分,则认为该用户对此教育机构授课方式“认可”,否则认为该用户对此教育机构授课方式“不认可”.
(1)请根据此样本完成下列2×2列联表,并据此列联表分析,能否有95%的把握认为城市经济状况与该市的用户认可该教育机构授课方式有关?
认可 | 不认可 | 合计 | |
A城市 | |||
B城市 | |||
合计 |
(2)以该样本中A,B城市的用户对此教育机构授课方式“认可”的频率分别作为A,B城市用户对此教育机构授课方式“认可”的概率.现从A城市和B城市的所有用户中分别随机抽取2个用户,用X表示这4个用户中对此教育机构授课方式“认可”的用户个数,求X的分布列.
参考公式: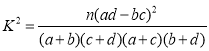 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() ,过其右焦点F的直线
,过其右焦点F的直线![]() 交椭圆C于M,N两点,交y轴于E点.若
交椭圆C于M,N两点,交y轴于E点.若![]() ,
,![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)试判断![]() 是否是定值.若是定值,求出该定值;若不是定值,请说明理由.
是否是定值.若是定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]()
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点.求![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com