
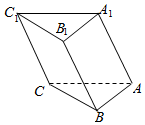
 如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC,且AB=AC=A1B=1.
如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC,且AB=AC=A1B=1.分析 (1)以A为原点,AC为x轴,AB为y轴,过A作平面ABC的垂线为z轴,建立空间直角坐标系,利用向量法能求出AA1与棱BC所成的角的大小.
(2)P为棱B1C1上一点,求出平面PAB的法向量和平面ABA1的法向量,利用向量法能求出P为棱B1C1中点.
解答  解:(1)如图,以A为原点,AC为x轴,AB为y轴,过A作平面ABC的垂线为z轴,建立空间直角坐标系,
解:(1)如图,以A为原点,AC为x轴,AB为y轴,过A作平面ABC的垂线为z轴,建立空间直角坐标系,
则C(1,0,0),B(0,1,0),A1(0,1,1),B1(0,2,1),
$\overrightarrow{A{A_1}}=(0,1,1)$,$\overrightarrow{BC}=\overrightarrow{{B_1}{C_1}}=(1,-1,0)$,(3分)
∴$cos<\overrightarrow{A{A_1}},\overrightarrow{BC}>=\frac{{\overrightarrow{A{A_1}}•\overrightarrow{BC}}}{{|{\overrightarrow{A{A_1}}}||{\overrightarrow{BC}}|}}=\frac{-1}{{\sqrt{2}•\sqrt{2}}}=-\frac{1}{2}$,
故AA1与棱BC所成的角是$\frac{π}{3}$.
(2)P为棱B1C1上一点,设$\overrightarrow{{B_1}P}=λ\overrightarrow{{B_1}{C_1}}=(λ,-λ,0)$,则P(λ,2-λ,1),
设平面PAB的法向量为$\overrightarrow{n_1}=(x,y,z)$,$\overrightarrow{AP}=(λ,2-λ,1)$,
则$\left\{{\begin{array}{l}{\overrightarrow{n_1}•\overrightarrow{AP}=0}\\{\overrightarrow{n_1}•\overrightarrow{AB}=0}\end{array}}\right.⇒\left\{{\begin{array}{l}{λx+z=0}\\{y=0}\end{array}}\right.⇒\left\{{\begin{array}{l}{z=-λx}\\{y=0}\end{array}}\right.$,则$\overrightarrow{n_1}=(1,0,-λ)$,(9分)
而平面ABA1的法向量是$\overrightarrow{n_2}=(1,0,0)$,
∴$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|{\overrightarrow{n_1}}||{\overrightarrow{n_2}}|}}=\frac{1}{{\sqrt{1+{λ^2}}}}=\frac{{2\sqrt{5}}}{5}$,解得$λ=\frac{1}{2}$,
即P为棱B1C1中点,其坐标为$P(\frac{1}{2},\frac{3}{2},1)$.(12分)
点评 本题考查异南在线所成角的大小的求法,考查满足条件的眯的位置的确定,是中档题,解题时要认真审题,注意向量法的合理运用.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 若该大学某女生身高增加1cm,则其体重约增加0.85kg | |
| B. | 回归直线过样本的中心($\overline{x}$,$\overline{y}$) | |
| C. | y与x具有正的线性相关关系 | |
| D. | 若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x∈R|0<x<$\frac{1}{2}$} | B. | {x∈R|$\frac{1}{2}$<x<1} | C. | {x∈R|0<x<1} | D. | {x∈R|x≠0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2$\sqrt{2}$)∪(2$\sqrt{2}$,+∞) | B. | (2$\sqrt{2}$,3) | C. | (2,3) | D. | (2$\sqrt{2}$,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 性别与是否喜欢理科无关 | B. | 女生中喜欢理科的比为80% | ||
| C. | 男生比女生喜欢理科的可能性大 | D. | 男生中喜欢理科的比例为80% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在犯错误的概率不超过0.05的前提下,认为打鼾与患心脏病有关 | |
| B. | 约有95%的打鼾者患心脏病 | |
| C. | 在犯错误的概率不超过0.01的前提下,认为打鼾与患心脏病有关 | |
| D. | 约有99%的打鼾者患心脏病 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com