
【题目】已知点![]() ,平面直角坐标系上的一个动点
,平面直角坐标系上的一个动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)点![]() 是曲线
是曲线![]() 上的任意一点,
上的任意一点,![]() 为圆
为圆![]() 的任意一条直径,求
的任意一条直径,求![]() 的取值范围;
的取值范围;
科目:高中数学 来源: 题型:
【题目】小王于年初用50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售价格为(25-x)万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大?(利润=累计收入+销售收入-总支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图.
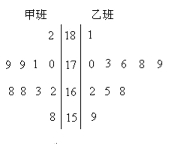
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过长期观测得到:在交通繁忙的时段内,某公路汽车的车流量![]() (千辆/
(千辆/ ![]() )与汽车的平均速度
)与汽车的平均速度![]() 之间的函数关系式为
之间的函数关系式为![]() .
.
(I)若要求在该段时间内车流量超过2千辆/ ![]() ,则汽车在平均速度应在什么范围内?
,则汽车在平均速度应在什么范围内?
(II)在该时段内,当汽车的平均速度![]() 为多少时,车流量最大?最大车流量为多少?
为多少时,车流量最大?最大车流量为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:22,23,25,26,31,30;若B样本数据恰好是A样本中每个数据都减去10后所得的数据,则A,B两样本的下列数字特征相同的是( )
A.方差B.平均数C.众数D.中位数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某隧道设计为双向四车道,车道总宽为![]() ,要求通行车辆限高
,要求通行车辆限高![]() ,隧道全长为
,隧道全长为![]() ,隧道的拱线可近似的看成半个椭圆形状.
,隧道的拱线可近似的看成半个椭圆形状.
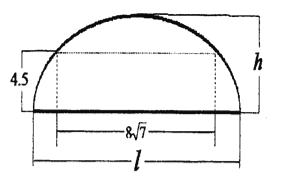
(1)若最大拱高![]() 为
为![]() ,则隧道设计的拱宽
,则隧道设计的拱宽![]() 是多少?
是多少?
(2)若最大拱高![]() 不小于
不小于![]() ,则应如何设计拱高
,则应如何设计拱高![]() 和拱宽
和拱宽![]() ,才能使隧道的土方工程量最小?
,才能使隧道的土方工程量最小?
(注: 1.半个椭圆的面积公式为![]() ;2.隧道的土方工程量=截面面积
;2.隧道的土方工程量=截面面积![]() 隧道长)
隧道长)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() .设圆
.设圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上.
上.
(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com