
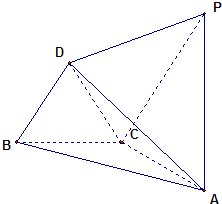
 已知△ABC与△DBC都是边长为
已知△ABC与△DBC都是边长为2
| ||
| 3 |
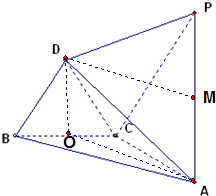 证明:(Ⅰ)取BC的中点O,连接DO,则DO⊥BC
证明:(Ⅰ)取BC的中点O,连接DO,则DO⊥BC| DM |
| PD |
| ||
| 2 |


科目:高中数学 来源: 题型:
 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使| AP |
| AE |
| PD |
| CD |
| AB |
| a |
| BC |
| b |
| a |
| b |
| BP |
查看答案和解析>>
科目:高中数学 来源: 题型:
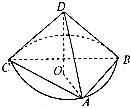 已知四面体ABCD中,DA=DB=DC=3
已知四面体ABCD中,DA=DB=DC=3| 2 |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修2) 2009-2010学年 第18期 总174期 人教课标高一版 题型:022
已知△ABC在平面α内,∠A=90°,DA⊥平面α,则CA与DB的位置关系是________.
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高一版(必修4) 2009-2010学年 第46期 总202期 北师大课标版 题型:044
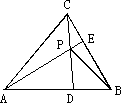
如下图,已知△ABC的面积为14 cm2,D,E分别为边AB,BC上的点,P是AE与CD的交点,且AD∶DB=BE∶EC=2∶1,求△APC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
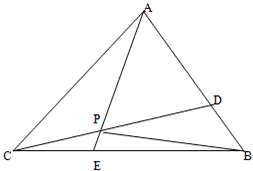 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使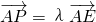 ,
,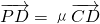 ,
,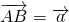 ,
,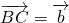 .
. ,
, 表示
表示 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com