
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化.某调查机构随机抽取8名购物者进行采访,4名男性购物者中有3名倾向于网购,1名倾向于选择实体店,4名女性购物者中有2名倾向于选择网购,2名倾向于选择实体店.
(1)若从8名购物者中随机抽取2名,其中男女各一名,求至少1名倾向于选择实体店的概率:
(2)若从这8名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品所得利润分别为![]() 和
和![]() (万元),它们与投入资金
(万元),它们与投入资金![]() (万元)的关系有如下公式:
(万元)的关系有如下公式:![]() ,
,![]() ,今将200万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于25万元.
,今将200万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于25万元.
(Ⅰ)设对乙种产品投入资金![]() (万元),求总利润
(万元),求总利润![]() (万元)关于
(万元)关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(Ⅱ)如何分配投入资金,才能使总利润最大,并求出最大总利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]()
满足:![]() 或1(k=1,2,…,n-1).
或1(k=1,2,…,n-1).
对任意i,j,都存在s,t,使得![]() ,其中i,j,s,t∈{1,2,…,n}且两两不相等.
,其中i,j,s,t∈{1,2,…,n}且两两不相等.
(I)若m=2,写出下列三个数列中所有符合题目条件的数列的序号;
①1,1,1,2,2,2; ②1,1,1,1,2,2,2,2; ③1,1,1,1,1,2,2,2,2
(II)记![]() .若m=3,求S的最小值;
.若m=3,求S的最小值;
(III)若m=2018,求n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(1-2x)(x2-2).
(1)求f(x)的单调区间和极值;
(2)若直线y=4x+b是函数y=f(x)图象的一条切线,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (a、b∈R,a、b为常数),且y=f(x)在x=1处切线方程为y=x﹣1.
(a、b∈R,a、b为常数),且y=f(x)在x=1处切线方程为y=x﹣1.
(1)求a,b的值;
(2)设h(x)=![]() , k(x)=2h′(x)x2 , 求证:当x>0时,k(x)<
, k(x)=2h′(x)x2 , 求证:当x>0时,k(x)<![]() +
+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中:
①若![]() ,满足
,满足![]() ,则
,则![]() 的最大值为4;
的最大值为4;
②若![]() ,则函数
,则函数![]() 的最小值为3;
的最小值为3;
③若![]() ,满足
,满足![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
④若![]() ,满足
,满足![]() ,则
,则![]() 的最小值为2;
的最小值为2;
⑤函数![]() 的最小值为9.
的最小值为9.
正确的有________.(把你认为正确的序号全部写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,第一象限内有定点
中,第一象限内有定点![]() 和射线
和射线![]() ,已知
,已知![]() ,
,![]() 的倾斜角分别为
的倾斜角分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 轴上的动点
轴上的动点![]() 与
与![]() ,
,![]() 共线.
共线.
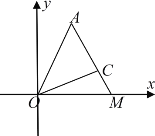
(1)求![]() 点坐标(用
点坐标(用![]() 表示);
表示);
(2)求![]() 面积
面积![]() 关于
关于![]() 的表达式
的表达式![]() ;
;
(3)求![]() 面积的最小时直线
面积的最小时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com