
给 个自上而下相连的正方形着黑色或白色. 当
个自上而下相连的正方形着黑色或白色. 当 时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案如图所示. 由此推断,当
时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案如图所示. 由此推断,当 时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种. (直接用数字作答)
时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种. (直接用数字作答)
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:填空题
如图1,小正方形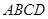 的面积为1,把它的各边延长一倍得到新正方形
的面积为1,把它的各边延长一倍得到新正方形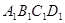 ,再把正方形
,再把正方形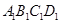 的各边延长一倍得到正方形
的各边延长一倍得到正方形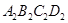 (如图2),如此进行下去,正方形
(如图2),如此进行下去,正方形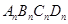 的面积为 .(用含有
的面积为 .(用含有 的式子表示,
的式子表示, 为正整数)
为正整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com