Question

【题目】若关于x的实系数方程x2+ax+b=0有两个根，一个根在区间（0，1）内，另一根在区间（1，3）内，记点（a，b）对应的区域为S．
（1）设z=2a﹣b，求z的取值范围；
（2）过点（﹣5，1）的一束光线，射到x轴被反射后经过区域S，求反射光线所在直线l经过区域S内的整点（即横纵坐标为整数的点）时直线l的方程．

Answer 1

【答案】
（1）解：解：方程x2+ax+b=0的两根在区间（0，1）和（1，3）上的几何意义是：

函数y=f（x）=x2+ax+b与x轴的两个交点的横坐标分别在区间（0，1）和（1，3）内，

由此可得不等式组

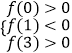，即 ，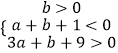

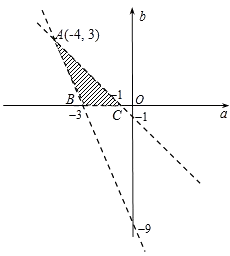
则在坐标平面aOb内，点（a，b）对应的区域S如图阴影部分所示，

易得图中A，B，C三点的坐标分别为（﹣4，3），（﹣3，0），（﹣1，0），

令z=2a﹣b，则直线b=2a﹣z经过点A时z取到下边界﹣11，经过点C时z取到上边界﹣2，又A，B，C三点的值没有取到，所以﹣11＜z＜﹣2；

（2）解：过点（﹣5，1）的光线经x轴反射后的光线必过点（﹣5，﹣1），由图可知

可能满足条件的整点为（﹣3，1），（﹣3，2），（﹣2，2），（﹣2，1），

再结合不等式知点（﹣3，1）符合条件，所以此时直线方程为：y+1= ﹣（x+5），

即y=x+4

【解析】（1）令f（x）=x2+ax+b，根据题意可知f（0）＞0，f（1）＜0，f（3）＞0，进而求得b＞0，a+b+1＜0，a+b+9＞0，画出可行域，进而分别求得z的最大和最小值，答案可得．（2）过点（﹣5，1）的光线经x轴反射后的光线必过点（﹣5，﹣1），由图可知，找出可能满足条件的整点，再结合不等式知点（﹣3，1）符合条件，得到此时直线方程即可．