
| A. | {x|$\frac{3}{4}$≤x≤2} | B. | {x|$\frac{3}{4}$≤x<2} | C. | {x|x<2} | D. | {x|x>2或x≤$\frac{3}{4}$} |
分析 通过讨论x-2的符号,求出不等式的解集即可.
解答 解:∵$\frac{3x-1}{2-x}≤1$,
∴$\frac{3x-1}{2-x}$-$\frac{2-x}{2-x}$≤0,
∴$\frac{4x-3}{x-2}$≥0,
故$\left\{\begin{array}{l}{4x-3≥0}\\{x-2>0}\end{array}\right.$或$\left\{\begin{array}{l}{4x-3≤0}\\{x-2<0}\end{array}\right.$,
解得:x>2或x≤$\frac{3}{4}$,
故不等式的解集是:{x|x>2或x≤$\frac{3}{4}$},
故选:D.
点评 本题考查了解分式不等式问题,是一道基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
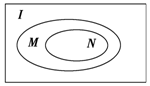
| A. | (∁IM)?(∁IN) | B. | M⊆(∁IN) | C. | (∁IM)⊆(∁IN) | D. | M?(∁IN) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
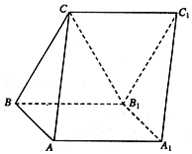 如图,三棱柱ABC-A1B1C1的侧面AA1B1B是边长为2的正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面AA1B1B是边长为2的正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x>1,则$\frac{1}{x}$<1”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
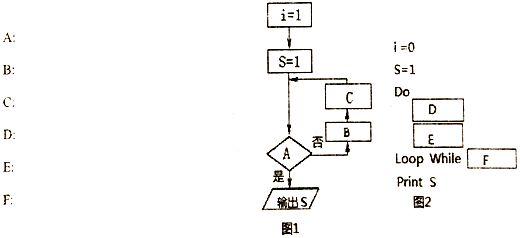
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com