[题目]已知△ABC中.内角A.B.C的对边分别为a.b.c.若a.b.c成等比数列.则的取值范围为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知△ABC中，内角A，B，C的对边分别为a，b，c，若a，b，c成等比数列，则的取值范围为．

【答案】[2, ）
【解析】解：a，b，c成等比数列，

设 = =q，q＞0，

则b=aq，c=aq2，

∴

∴ ，

解得＜q＜．

则 = + = +q，

由f（q）= +q在（，1）递减，在（1，）递增，

可得f（1）取得最小值2，由f（）=f（）= ，

即有f（q）∈[2，）．

所以答案是：[2，）．

【考点精析】通过灵活运用函数的最值及其几何意义和等比数列的通项公式（及其变式），掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值；通项公式：即可以解答此题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知圆C的圆心在射线y=2x﹣3（x≥0），且与直线y=x+2和y=﹣x+4都相切．
（1）求圆C的方程；
（2）若P（x，y）是圆C上任意一点，求x+2y的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知一组数据3，4，5，a，b的平均数是4，中位数是m，从3，4，5，a，b，m这组数据中任取一数，取到数字4的概率为，那么3，4，5，a，b这组数据的方差为（）
A.
B.2
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】儿童乘坐火车时，若身高不超过1.1m，则不需买票；若身高超过1.1m但不超过1.4m，则需买半票；若身高超过1.4m，则需买全票．试设计一个买票的算法，并写出相应的程序．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】圆x2+y2=8内有一点P0（﹣1，2），AB为过点P0且倾斜角为α的弦；
（1）当时，求AB的长；
（2）当弦AB被点P0平分时，求直线AB的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某学校为了解学校食堂的服务情况，随机调查了50名就餐的教师和学生．根据这50名师生对餐厅服务质量进行评分，绘制出了频率分布直方图（如图所示），其中样本数据分组为[40，50），[50，60），…，[90，100]．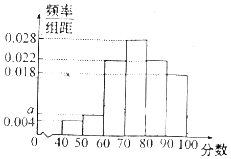
（1）求频率分布直方图中a的值；
（2）从评分在[40，60）的师生中，随机抽取2人，求此人中恰好有1人评分在[40，50）上的概率；
（3）学校规定：师生对食堂服务质量的评分不得低于75分，否则将进行内部整顿，试用组中数据估计该校师生对食堂服务质量评分的平均分，并据此回答食堂是否需要进行内部整顿．