
分析 是结合复合函数单调性的关系进行判断.
②根据基本由函数奇偶性的定义判断函数为偶函数判断;
③利用对勾函数的单调性判断;
④由对勾函数的最值及函数奇偶性的性质进行判断即可.
解答 解:①函数f(x)=lg$\frac{{{x^2}+1}}{|x|}$,(x∈R且x≠0).
∵$\frac{{{x^2}+1}}{|x|}$$≥\frac{2|x|}{|x|}$=2,
∴f(x)=lg$\frac{{{x^2}+1}}{|x|}$≥2,即f(x)的最小值是lg2,故①正确,
②∵f(-x)=$lg\frac{(-x)^{2}+1}{|-x|}=lg\frac{{x}^{2}+1}{|x|}$=f(x),∴函数f(x)为偶函数,图象关于y轴对称,故②正确;
③当x>0时,t(x)=$\frac{{x}^{2}+1}{|x|}=\frac{{x}^{2}+1}{x}=x+\frac{1}{x}$,在(0,1)上单调递减,在(1,+∞)上得到递增,
∴f(x)=lg$\frac{{{x^2}+1}}{|x|}$在(0,1)上单调递减,在(1,+∞)上得到递增,故③错误;
④∵函数f(x)是偶函数,由③知f(x)在(0,1)上单调递减,在(1,+∞)上得到递增,
∴在(-1,0)上单调递增,在(-∞,-1)上得到递减,故④正确,
故答案为:①②④
点评 本题考查了命题的真假判断与应用,考查了函数奇偶性的性质,考查了复合函数的单调性,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
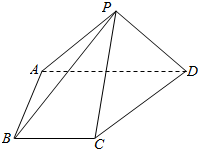 如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是$\frac{8π}{3}$.(结果保留π)
如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是$\frac{8π}{3}$.(结果保留π)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -36 | B. | -30 | C. | -27 | D. | -20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$] | C. | (-∞,0)∪(0,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com