
【题目】为了迎接2019年的高考,某学校进行了第一次模拟考试,其中五个班的考试成绩在500分以上的人数如下表,![]() 为班级,
为班级,![]() 表示500分以上的人数
表示500分以上的人数
| 1 | 2 | 3 | 4 | 5 |
| 20 | 25 | 30 | 30 | 25 |
(1)若给出数据,班级![]() 与考试成绩500以上的人数
与考试成绩500以上的人数![]() ,满足回归直线方程
,满足回归直线方程![]() ,求出该回归直线方程;
,求出该回归直线方程;
(2)学校为了更好的提高学生的成绩,了解一模的考试成绩,从考试成绩在500分以上1,3班学生中,利用分层抽样抽取5人进行调研,再从选中的5人中,再选3名学生写出“经验介绍”文章,则选的三名学生1班一名,3班2名的概率.
参考公式: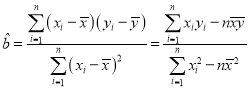 ,
,![]() .
.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】将4名大学生随机安排到A,B,C,D四个公司实习.
(1)求4名大学生恰好在四个不同公司的概率;
(2)随机变量X表示分到B公司的学生的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
![]()
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
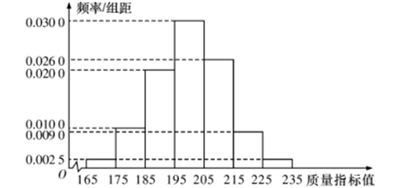
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品![]() ”的规定?
”的规定?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 对任意
对任意![]() 都有
都有![]() (其中
(其中![]() 、
、![]() 、
、![]() 是常数) .
是常数) .
(Ⅰ)当![]() ,
,![]() ,
,![]() 时,求
时,求![]() ;
;
(Ⅱ)当![]() ,
,![]() ,
,![]() 时,若
时,若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若数列![]() 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.当
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.当![]() ,
,![]() ,
,![]() 时,设
时,设![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() ,试问:是否存在这样的“封闭数列”,使得对任意
,试问:是否存在这样的“封闭数列”,使得对任意![]() ,都有
,都有![]() ,且
,且![]() .若存在,求数列
.若存在,求数列![]() 的首项
的首项![]() 的所有取值;若不存在,说明理由.
的所有取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展.据统 计,在2018年这一年内从![]() 市到
市到![]() 市乘坐高铁或飞机出行的成年人约为
市乘坐高铁或飞机出行的成年人约为![]() 万人次.为了 解乘客出行的满意度,现从中随机抽取
万人次.为了 解乘客出行的满意度,现从中随机抽取![]() 人次作为样本,得到下表(单位:人次):
人次作为样本,得到下表(单位:人次):
满意度 | 老年人 | 中年人 | 青年人 | |||
乘坐高铁 | 乘坐飞机 | 乘坐高铁 | 乘坐飞机 | 乘坐高铁 | 乘坐飞机 | |
10分(满意) | 12 | 1 | 20 | 2 | 20 | 1 |
5分(一般) | 2 | 3 | 6 | 2 | 4 | 9 |
0分(不满意) | 1 | 0 | 6 | 3 | 4 | 4 |
(1)在样本中任取![]() 个,求这个出行人恰好不是青年人的概率;
个,求这个出行人恰好不是青年人的概率;
(2)在2018年从![]() 市到
市到![]() 市乘坐高铁的所有成年人中,随机选取
市乘坐高铁的所有成年人中,随机选取![]() 人次,记其中老年人出行的人次为
人次,记其中老年人出行的人次为![]() .以频率作为概率,求
.以频率作为概率,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)如果甲将要从![]() 市出发到
市出发到![]() 市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机? 并说明理由.
市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机? 并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,满足
上一点,满足![]() ,
,![]() 为
为![]() 的中点,现将梯形沿
的中点,现将梯形沿![]() 折叠(如图2),使平面
折叠(如图2),使平面![]() 平面
平面![]() .
.
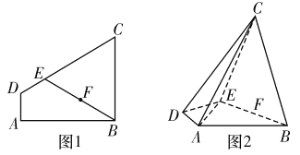
(1)求证:平面![]() 平面
平面![]() ;
;
(2)能否在线段![]() 上找到一点
上找到一点![]() (端点除外)使得直线
(端点除外)使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体B-ACDE中,AB⊥AC,AB=4,AC=3,DC⊥平面ABC,EA⊥平面ABC,点M在线段BC上,且AM=![]() .
.
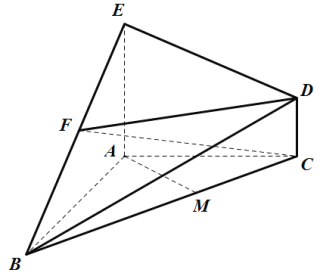
(1)证明:AM⊥平面BCD;
(2)若点F为线段BE的中点,且三棱锥F-BCD的体积为1,求CD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
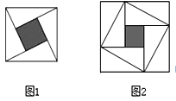
【题目】赵爽弦图(图1)是取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.图2是由弦图变化得到,它是由八个全等的直角三角形和中间的一个小正方形拼接而成.现随机向图2中大正方形的内部投掷一枚飞镖,若直角三角形的直角边长分别为2和3,则飞镖投中小正方形(阴影)区域的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com