
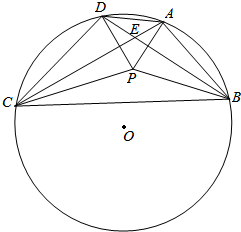
 凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线. 分析 圆O内有一点K,A1B1、A2B2、A3B3、A4B4是过K的圆O的弦,若A1A2∩A3A4=M,B1B2∩B3B4=N,则K,M,N三点共线,由此能证明O,P,E三点共线.
解答 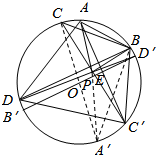 证明:引理:圆O内有一点K,A1B1、A2B2、A3B3、A4B4是过K的圆O的弦,
证明:引理:圆O内有一点K,A1B1、A2B2、A3B3、A4B4是过K的圆O的弦,
若A1A2∩A3A4=M,B1B2∩B3B4=N,则K,M,N三点共线.
引理的证明:在圆O所在的实射影平面内考虑这样一个射影变换,
它把圆O变为圆,把K为圆心,K的像记为k′等等,
则由圆K′的对称性,${{A}_{1}}^{'}{{A}_{2}}^{'}$与${{B}_{1}}^{'}{{B}_{2}}^{'}$关于K′中心对称,${{A}_{3}}^{'}{{A}_{4}}^{'}$与${{B}_{3}}^{'}{{B}_{4}}^{'}$关于K′中心对称,
故M′与N′关于K′中心对称,从而K′、M′、N′三点共线,
由射影变换性质,得原来K、M、N三点共线.
下面回到本题:
延长AP、BP、CP、DP分别交⊙O于A′、B′、C′、D′,
连结A′C′、B′D′、A‘B、BC’,
则∠A′C′B+∠CA′B=∠A′AB+∠C′CB=90°,
∴∠A′BC′=90°,A′C′为直径,同理B′D′为直径,
∵A不与D、D重合,A′C′不与B′D′重合,∴A′C′∩B′D′=O,
在引理中,令K=P,A1=A,A2=C,B1=B,B2=D,即得到O、P、E三点共线,
∴O、P、E共线.
点评 本题考查与圆有关的三点共线的证明,综合性强,难度较大,解题时要注意射影性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
| 老年 | 40 | 40 | 40 | 80 | 200 |
| 中年 | 80 | 120 | 160 | 240 | 600 |
| 青年 | 40 | 160 | 280 | 720 | 1 200 |
| 小计 | 160 | 320 | 480 | 1 040 | 2 000 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c≥4 | B. | c≥3 | C. | c≥2 | D. | c≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com