
【题目】△ABC中,角A,B,C所对应的分别为a,b,c,且(a+b)(sinA﹣sinB)=(c﹣b)sinC,若a=2,则△ABC的面积的最大值是( )
A.1B.![]() C.2D.2
C.2D.2![]()
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】某高三理科班共有60名同学参加某次考试,从中随机挑选出5名同学,他们的数学成绩x与物理成绩y如下表:

数据表明y与x之间有较强的线性关系.
(1)求y关于x的线性回归方程;
(2)该班一名同学的数学成绩为110分,利用(1)中的回归方程,估计该同学的物理成绩;
(3)本次考试中,规定数学成绩达到125分为优秀,物理成绩达到100分为优秀.若该班数学优秀率与物理优秀率分别为50%和60%,且除去抽走的5名同学外,剩下的同学中数学优秀但物理不优秀的同学共有5人.能否在犯错误概率不超过0.01的前提下认为数学优秀与物理优秀有关?
参考数据:回归直线的系数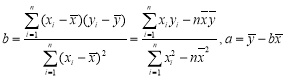 .
.
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
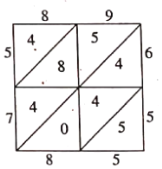
【题目】写算,是一种格子乘法,也是笔算乘法的一种,用以区别筹算与珠算,它由明代数学家吴敬在其撰写的《九章算法比类大全》一书中提出,是从天元式的乘法演变而来.例如计算![]() ,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出
,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出![]() 的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .记
.记![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 上的点到
上的点到![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为数列{an}的前n项和,且Sn+2=2an,n∈N*.
(1)求数列{an}的通项公式;
(2)令bn![]() ,设数列{bn}的前项和为Tn,若Tn
,设数列{bn}的前项和为Tn,若Tn![]() ,求n的最小值.
,求n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 图象上的各点的横坐标缩短到原来的
图象上的各点的横坐标缩短到原来的![]() ,纵坐标不变,再向左平移
,纵坐标不变,再向左平移![]() 个单位,得到
个单位,得到![]() 的图象,下列说法正确的是( )
的图象,下列说法正确的是( )
A.点![]() 是函数
是函数![]() 图象的对称中心
图象的对称中心
B.函数![]() 在
在![]() 上单调递减
上单调递减
C.函数![]() 的图象与函数
的图象与函数![]() 的图象相同
的图象相同
D.若![]() ,
,![]() 是函数的零点,则
是函数的零点,则![]() 是
是![]() 的整数倍
的整数倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司以客户满意为出发点,随机抽选2000名客户,以调查问卷的形式分析影响客户满意度的各项因素.每名客户填写一个因素,下图为客户满意度分析的帕累托图.帕累托图用双直角坐标系表示,左边纵坐标表示频数,右边纵坐标表示频率,分析线表示累计频率,横坐标表示影响满意度的各项因素,按影响程度(即频数)的大小从左到右排列,以下结论正确的个数是( ).
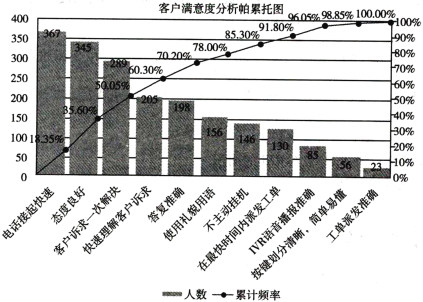
①35.6%的客户认为态度良好影响他们的满意度;
②156位客户认为使用礼貌用语影响他们的满意度;
③最影响客户满意度的因素是电话接起快速;
④不超过10%的客户认为工单派发准确影响他们的满意度.
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com