
【题目】已知椭圆C:![]() ,
,![]() 分别是其左、右焦点,过
分别是其左、右焦点,过![]() 的直线l与椭圆C交于A,B两点,且椭圆C的离心率为
的直线l与椭圆C交于A,B两点,且椭圆C的离心率为![]() ,
,![]() 的内切圆面积为
的内切圆面积为![]() ,
,![]() .
.
(I)求椭圆C的方程;
(II)若![]() 时,求直线l的方程
时,求直线l的方程
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为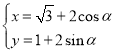 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,且长度单位相同.
轴的正半轴为极轴建立极坐标系,且长度单位相同.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() :
:![]() (
(![]() 为参数)被圆
为参数)被圆![]() 截得的弦长为2,求直线
截得的弦长为2,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位科技活动纪念章的结构如图所示,O是半径分别为1cm,2cm的两个同心圆的圆心,等腰△ABC的顶点A在外圆上,底边BC的两个端点都在内圆上,点O,A在直线BC的同侧.若线段BC与劣弧![]() 所围成的弓形面积为S1,△OAB与△OAC的面积之和为S2, 设∠BOC=2
所围成的弓形面积为S1,△OAB与△OAC的面积之和为S2, 设∠BOC=2![]() .
.

(1)当![]() 时,求S2﹣S1的值;
时,求S2﹣S1的值;
(2)经研究发现当S2﹣S1的值最大时,纪念章最美观,求当纪念章最美观时,cos![]() 的值.(求导参考公式:(sin2x)'=2cos2x,(cos2x)'=﹣2sin2x)
的值.(求导参考公式:(sin2x)'=2cos2x,(cos2x)'=﹣2sin2x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,一方有难八方支援,全国各地的白衣天使走上战场的第一线,某医院抽调甲、乙两名医生,抽调![]() 、
、![]() 、
、![]() 三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士
三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士![]() 被选在第一医院工作的概率为( )
被选在第一医院工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数据的收集和整理在当今社会起到了举足轻重的作用,它用统计的方法来帮助人们分析以往的行为习惯,进而指导人们接下来的行动.
某支足球队的主教练打算从预备球员甲、乙两人中选一人为正式球员,他收集到了甲、乙两名球员近期5场比赛的传球成功次数,如下表:
场次 | 第一场 | 第二场 | 第三场 | 第四场 | 第五场 |
甲 | 28 | 33 | 36 | 38 | 45 |
乙 | 39 | 31 | 43 | 39 | 33 |
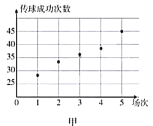
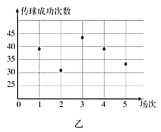
(1)根据这两名球员近期5场比赛的传球成功次数,完成茎叶图(茎表示十位,叶表示个位);分别在平面直角坐标系中画出两名球员的传球成功次数的散点图;
(2)求出甲、乙两名球员近期5场比赛的传球成功次数的平均值和方差;
(3)主教练根据球员每场比赛的传球成功次数分析出球员在场上的积极程度和技术水平,同时根据多场比赛的数据也可以分析出球员的状态和潜力.你认为主教练应选哪位球员?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别为B1C1,C1D1的中点,点P是上底面A1B1C1D1内一点,且AP∥平面EFDB,则cos∠APA1的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象如图所示,先将函数
的图象如图所示,先将函数![]() 图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移
图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,下列结论正确的是( )
的图象,下列结论正确的是( )
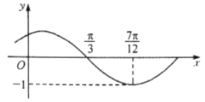
A.函数![]() 是奇函数B.函数
是奇函数B.函数![]() 在区间
在区间![]() 上是增函数
上是增函数
C.函数![]() 图象关于
图象关于![]() 对称D.函数
对称D.函数![]() 图象关于直线
图象关于直线![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动,在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论(素数即质数,
的结论(素数即质数,![]() ).根据欧拉得出的结论,如下流程图中若输入
).根据欧拉得出的结论,如下流程图中若输入![]() 的值为
的值为![]() ,则输出
,则输出![]() 的值应属于区间( )
的值应属于区间( )
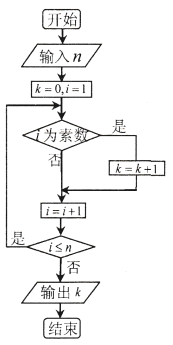
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点
于点![]() ,交棱
,交棱![]() 于点
于点![]() ,下列正确的是( )
,下列正确的是( )
A.平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
B.四边形![]() 一定是平行四边形;
一定是平行四边形;
C.平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
D.四边形![]() 的面积有最大值.
的面积有最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com