
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的单调区间;
的单调区间;
(3)当![]() 时,求函数
时,求函数![]() 在上区间
在上区间![]() 零点的个数.
零点的个数.
科目:高中数学 来源: 题型:
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:
年龄x | 28 | 32 | 38 | 42 | 48 | 52 | 58 | 62 |
收缩压 | 114 | 118 | 122 | 127 | 129 | 135 | 140 | 147 |
其中: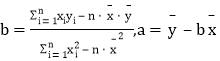 ,
,![]() ,
,![]()
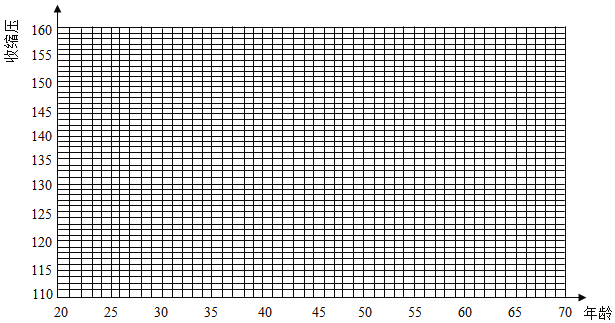
![]() 请画出上表数据的散点图;
请画出上表数据的散点图;
![]() 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;![]() 的值精确到
的值精确到![]()
![]() 若规定,一个人的收缩压为标准值的
若规定,一个人的收缩压为标准值的![]() 倍,则为血压正常人群;收缩压为标准值的
倍,则为血压正常人群;收缩压为标准值的![]() 倍,则为轻度高血压人群;收缩压为标准值的
倍,则为轻度高血压人群;收缩压为标准值的![]() 倍,则为中度高血压人群;收缩压为标准值的
倍,则为中度高血压人群;收缩压为标准值的![]() 倍及以上,则为高度高血压人群
倍及以上,则为高度高血压人群![]() 一位收缩压为180mmHg的70岁的老人,属于哪类人群?
一位收缩压为180mmHg的70岁的老人,属于哪类人群?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:①如果向量![]() 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么![]() 的关系是不共线;②
的关系是不共线;②![]() 为空间四点,且向量
为空间四点,且向量![]() 不构成空间的一个基底,那么点
不构成空间的一个基底,那么点![]() 一定共面;③已知向量
一定共面;③已知向量![]() 是空间的一个基底,则向量
是空间的一个基底,则向量![]() ,也是空间的一个基底。其中正确的命题是( )
,也是空间的一个基底。其中正确的命题是( )
A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游戏公司对今年新开发的一些游戏进行评测,为了了解玩家对游戏的体验感,研究人员随机调查了300名玩家,对他们的游戏体验感进行测评,并将所得数据统计如图所示,其中![]() .
.

(1)求这300名玩家测评分数的平均数;
(2)由于该公司近年来生产的游戏体验感较差,公司计划聘请3位游戏专家对游戏进行初测,如果3人中有2人或3人认为游戏需要改进,则公司将回收该款游戏进行改进;若3人中仅1人认为游戏需要改进,则公司将另外聘请2位专家二测,二测时,2人中至少有1人认为游戏需要改进的话,公司则将对该款游戏进行回收改进.已知该公司每款游戏被每位专家认为需要改进的概率为![]() ,且每款游戏之间改进与否相互独立.
,且每款游戏之间改进与否相互独立.
(i)对该公司的任意一款游戏进行检测,求该款游戏需要改进的概率;
(ii)每款游戏聘请专家测试的费用均为300元/人,今年所有游戏的研发总费用为50万元,现对该公司今年研发的600款游戏都进行检测,假设公司的预算为110万元,判断这600款游戏所需的最高费用是否超过预算,并通过计算说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体中,四边形![]() 和
和![]() 都为矩形.
都为矩形.

(1)若![]() ,证明:直线
,证明:直线![]() 平面
平面![]() ;
;
(2)设![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 平面
平面![]() ?请证明你的结论.
?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(2)若![]() ,关于
,关于![]() 的方程
的方程![]() 有且仅有一个根, 求实数
有且仅有一个根, 求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,不等式
,不等式![]() 均成立, 求实数
均成立, 求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com