
【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
科目:高中数学 来源: 题型:
【题目】某儿童节在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.记两次记录的数分别为x,y.奖励规则如下:
①若xy≤3,则奖励玩具一个;
②若xy≥8,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.
(1)求小亮获得玩具的概率;
(2)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=a(x﹣2)ex+lnx+ ![]() 在(0,2)上存在两个极值点,则a的取值范围为( )
在(0,2)上存在两个极值点,则a的取值范围为( )
A.(﹣∞,﹣ ![]() )
)
B.(﹣ ![]() ,
, ![]() )∪(1,+∞)
)∪(1,+∞)
C.(﹣∞,﹣ ![]() )
)
D.(﹣∞,﹣ ![]() )∪(﹣﹣
)∪(﹣﹣ ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图像,只要将
上的图象,为了得到这个函数的图像,只要将![]() 的图象上所有的点 ( )
的图象上所有的点 ( )

A. 向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
B. 向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C. 向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
D. 向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦距为2的椭圆W: ![]() =1(a>b>0)的左、右焦点分别为A1 , A2 , 上、下顶点分别为B1 , B2 , 点M(x0 , y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1 , MA2 , MB1 , MB2的斜率之积为
=1(a>b>0)的左、右焦点分别为A1 , A2 , 上、下顶点分别为B1 , B2 , 点M(x0 , y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1 , MA2 , MB1 , MB2的斜率之积为 ![]() .
.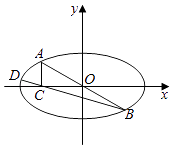
(1)求椭圆W的标准方程;
(2)如图所示,点A,D是椭圆W上两点,点A与点B关于原点对称,AD⊥AB,点C在x轴上,且AC与x轴垂直,求证:B,C,D三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com