
【题目】给图中A,B,C,D,E,F六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有4种颜色可供选择,则共有___种不同的染色方案.

【答案】96
【解析】
通过分析题目给出的图形,可知要完成给图中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六个区域进行染色,最少需要3种颜色,即
六个区域进行染色,最少需要3种颜色,即![]() 同色,
同色,![]() 同色,
同色,![]() 同色,由排列知识可得该类染色方法的种数;也可以4种颜色全部用上,即
同色,由排列知识可得该类染色方法的种数;也可以4种颜色全部用上,即![]() ,
,![]() ,
,![]() 三组中有一组不同色,同样利用排列组合知识求解该种染法的方法种数,最后利用分类加法求和.
三组中有一组不同色,同样利用排列组合知识求解该种染法的方法种数,最后利用分类加法求和.
解:要完成给图中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六个区域进行染色,染色方法可分两类,第一类是仅用三种颜色染色,
六个区域进行染色,染色方法可分两类,第一类是仅用三种颜色染色,
即![]() 同色,
同色,![]() 同色,
同色,![]() 同色,则从四种颜色中取三种颜色有
同色,则从四种颜色中取三种颜色有![]() 种取法,三种颜色染三个区域有
种取法,三种颜色染三个区域有![]() 种染法,共
种染法,共![]() 种染法;
种染法;
第二类是用四种颜色染色,即![]() ,
,![]() ,
,![]() 中有一组不同色,则有3种方案
中有一组不同色,则有3种方案![]() 不同色或
不同色或![]() 不同色或
不同色或![]() 不同色),先从四种颜色中取两种染同色区有
不同色),先从四种颜色中取两种染同色区有![]() 种染法,剩余两种染在不同色区有2种染法,共有
种染法,剩余两种染在不同色区有2种染法,共有![]() 种染法.
种染法.
![]() 由分类加法原理得总的染色种数为
由分类加法原理得总的染色种数为![]() 种.
种.
故答案为:96.


科目:高中数学 来源: 题型:
【题目】在△ABC中,A、B、C所对的边分别是a、b、c,且有bcosC+ccosB=2acosB.
(1)求B的大小;
(2)若△ABC的面积是![]() ,且a+c=5,求b.
,且a+c=5,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人在塔的正东方向上的![]() 处在与塔垂直的水平面内沿南偏西
处在与塔垂直的水平面内沿南偏西![]() 的方向以每小时
的方向以每小时![]() 千米的速度步行了
千米的速度步行了![]() 分钟以后,在点
分钟以后,在点![]() 处望见塔的底端
处望见塔的底端![]() 在东北方向上,已知沿途塔的仰角
在东北方向上,已知沿途塔的仰角![]() ,
,![]() 的最大值为
的最大值为![]() .
.
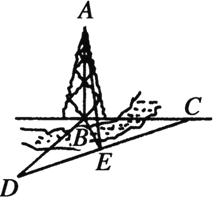
(1)求该人沿南偏西![]() 的方向走到仰角
的方向走到仰角![]() 最大时,走了几分钟;
最大时,走了几分钟;
(2)求塔的高![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线l过点![]() .
.
(1)若直线l的纵截距和横截距相等,求直线l的方程;
(2)若直线l与两坐标轴围成的三角形的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
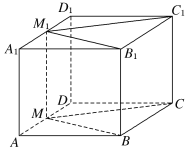
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com