
【题目】小李大学毕业后选择自主创业,开发了一种新型电子产品.2019年9月1日投入市场销售,在9月份的30天内,前20天每件售价![]() (元)与时间
(元)与时间![]() (天,
(天,![]() )满足一次函数关系,其中第一天每件售价为63元,第10天每件售价为90元;后10天每件售价均为120元.已知日销售量
)满足一次函数关系,其中第一天每件售价为63元,第10天每件售价为90元;后10天每件售价均为120元.已知日销售量![]() (件)与时间
(件)与时间![]() (天)之间的函数关系是
(天)之间的函数关系是![]() .
.
(1)写出该电子产品9月份每件售价![]() (元)与时间
(元)与时间![]() (天)的函数关系式;
(天)的函数关系式;
(2)9月份哪一天的日销售金额最大?并求出最大日销售金额.(日销售金额=每件售价![]() 日销售量).
日销售量).
【答案】(1)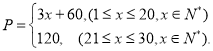 ;
;
(2)9月份第10天的日销售金额最大,最大为3675元.
【解析】
(1)设前20天每件售价P(元)与时间x(天,x∈N+)的解析式为P=kx+b,由条件列出方程,解方程可得k,b,进而运用分段函数的解析式可得所求;
(2)运用分段函数的形式写出9月份日销售金额的解析式,再由二次函数和一次函数的性质,即可得到所求最大值.
(1)设前20天每件售价![]() (元)与时间
(元)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() .
.
由题意得 ![]()
解得 ![]()
故该电子产品9月份每件售价![]() (元)与时间
(元)与时间![]() (天)的函数关系式为
(天)的函数关系式为
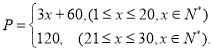
(2)设9月份日销售金额为![]() 元,则有
元,则有
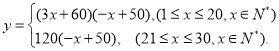
①当![]() 时,
时,![]() 的对称轴为
的对称轴为![]() .
.
![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数.
上为减函数.
![]() 当
当![]() 时,
时,![]()
②当![]() 时,
时,![]() 为减函数.
为减函数.
![]() 当
当![]() 时,
时,![]()
综上所述,9月份第10天的日销售金额最大,最大为3675元.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】选用适当的符号填空:
(1)若集合![]() ,则-4__________B,-3______A, A ___________B,B_________________A;
,则-4__________B,-3______A, A ___________B,B_________________A;
(2)若集合![]() ,则1__________A,
,则1__________A,![]() _______________A,
_______________A,![]() _________A;
_________A;
(3){![]() 是菱形}_____________{
是菱形}_____________{![]() 是平行四边形};{
是平行四边形};{![]() 是等腰三角形}_____________{
是等腰三角形}_____________{![]() 是等边三角形}.
是等边三角形}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 中,若
中,若![]() ,则下列命题中真命题个数是( )
,则下列命题中真命题个数是( )
(1)若数列![]() 为常数数列,则
为常数数列,则![]() ;
;
(2)若![]() ,数列
,数列![]() 都是单调递增数列;
都是单调递增数列;
(3)若![]() ,任取
,任取![]() 中的
中的![]() 项
项![]() 构成数列
构成数列![]() 的子数
的子数![]() (
(![]() ),则
),则![]() 都是单调数列.
都是单调数列.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 对于任意的
对于任意的![]() 都有
都有![]() ,给出以下命题:
,给出以下命题:
①![]() 在
在![]() 上是增函数;
上是增函数;
②可能存在![]() ,使得对任意的
,使得对任意的![]() 恒成立;
恒成立;
③可能存在![]() ,使得
,使得![]() 成立;
成立;
④![]() 没有最大值和最小值.
没有最大值和最小值.
则正确的命题的个数为( ).
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() :
:
(1)若![]() ,求y=f(x)的最大值和最小值,并写出相应的x值;
,求y=f(x)的最大值和最小值,并写出相应的x值;
(2)将函数y=f(x)的图象向右平移![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象,区间[a,b](a,b∈R且a<b)满足:y=g(x)在[a,b]上至少含有20个零点,在所有满足上述条件的[a,b]中,求b﹣a的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象,区间[a,b](a,b∈R且a<b)满足:y=g(x)在[a,b]上至少含有20个零点,在所有满足上述条件的[a,b]中,求b﹣a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() :
:![]() ,
,![]() 为平面上的动点,过点
为平面上的动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且满足
,且满足![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为直线
为直线![]() 上一点,且满足
上一点,且满足![]() ,若
,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2–a–lnx,g(x)=![]() ,其中a∈R,e=2.718…为自然对数的底数.
,其中a∈R,e=2.718…为自然对数的底数.
(1)讨论f(x) 的单调性;
(2)证明:当x>1时,g(x)>0;
(3)如果f(x)>g(x) 在区间(1,+∞)内恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①命题:“在![]() 中,若
中,若![]() 则
则![]() ”的逆命题为假命题;
”的逆命题为假命题;
②“![]() ”是直线
”是直线![]() 与圆
与圆![]() 相交的充分不必要条件;
相交的充分不必要条件;
③命题:“若![]() 则
则![]() ”的逆否命题是“若
”的逆否命题是“若![]() 则
则![]() ”;
”;
④若![]() 或
或![]() ,则
,则![]() 为真命题。
为真命题。
其中正确的说法个数为()
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且方程
,且方程![]() 有两个相等的实数根
有两个相等的实数根
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() 是
是![]() 上的奇函数,且
上的奇函数,且![]() 时,
时,![]() ,求
,求![]() 的解析式;
的解析式;
(3)若不等式![]() 对一切实数
对一切实数![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com