
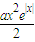 对于n∈R恒成立.
对于n∈R恒成立.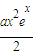 成立?如果存在,求出符合条件的一个x;否则说明理由.
成立?如果存在,求出符合条件的一个x;否则说明理由.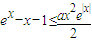 成立;(Ⅱ)在x≤0时,要使
成立;(Ⅱ)在x≤0时,要使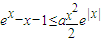 成立.利用导数研究函数的单调性,从而得到,原不等式
成立.利用导数研究函数的单调性,从而得到,原不等式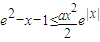 在a≥1时,恒成立;
在a≥1时,恒成立;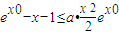 变形为
变形为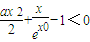 ,要找一个X>0,使此式成立,只需找到函数
,要找一个X>0,使此式成立,只需找到函数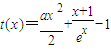 的最小值,满足t(x)min<0即可,对t(x)求导数,研究其单调性和最值,最后得出可找到一个常数x=-lna(0<a<1),使得不等式成立.
的最小值,满足t(x)min<0即可,对t(x)求导数,研究其单调性和最值,最后得出可找到一个常数x=-lna(0<a<1),使得不等式成立.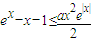 成立.
成立.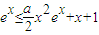 即需证:
即需证: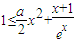 ①
①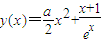 ,求导数
,求导数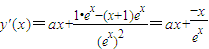
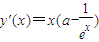 ,又a≥1,求x≥0,故y'(x)≥0
,又a≥1,求x≥0,故y'(x)≥0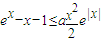 成立.
成立.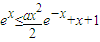 ,即需证:
,即需证: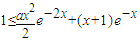 ②
②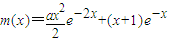 ,求导数得m'(x)=-xe-2x[ex+a(x-1)]
,求导数得m'(x)=-xe-2x[ex+a(x-1)]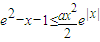 在a≥1时,恒成立…(6分)
在a≥1时,恒成立…(6分)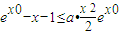 变形为
变形为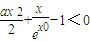 ③
③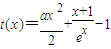 的最小值,
的最小值,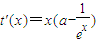
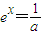 ,则x=-lna,取X=-lna
,则x=-lna,取X=-lna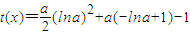
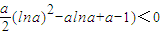 ,在0<a<1时成立即可
,在0<a<1时成立即可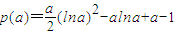 ,对p(a)关于a求导数
,对p(a)关于a求导数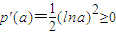 ,从而p(a)为增函数
,从而p(a)为增函数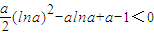 得证
得证

 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
| x1+x2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ln|x| |
| |x| |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ax2e|x| |
| 2 |
| ax02ex0 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省扬州中学高一(上)期中数学试卷(解析版) 题型:解答题
 ,则称f(x)是R上凹函数.已知二次函数f(x)=ax2+x(a∈R,且a≠0).
,则称f(x)是R上凹函数.已知二次函数f(x)=ax2+x(a∈R,且a≠0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com