
【题目】已知![]() ,函数
,函数![]() 在点
在点![]() 处与
处与![]() 轴相切
轴相切
(1)求![]() 的值,并求
的值,并求![]() 的单调区间;
的单调区间;
(2)当![]() 时,
时,![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
【答案】(1)见解析(2)![]()
【解析】
(1)求出函数的导数,利用已知条件列出方程,求出![]() ,判断导函数的符号,然后求解单调区间.
,判断导函数的符号,然后求解单调区间.
(2)令![]() ,
,![]() .求出
.求出![]() ,令
,令![]() ,求出导数,通过(i)若
,求出导数,通过(i)若![]() ,(ii)若
,(ii)若![]() ,判断函数的单调性求解最值,然后求解
,判断函数的单调性求解最值,然后求解![]() 的取值范围.
的取值范围.
(Ⅰ)函数![]() 在点
在点![]() 处与
处与![]() 轴相切.
轴相切.![]() ,
,
依题意,![]() 解得
解得![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)令![]() ,
,![]() .则
.则![]() ,
,
令![]() ,则
,则![]() ,
,
(ⅰ)若![]() ,因为当
,因为当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() 即
即![]() 在
在![]() 上单调递增.又因为
上单调递增.又因为![]() ,
,
所以当![]() 时,
时,![]() ,从而
,从而![]() 在
在![]() 上单调递增,
上单调递增,
而![]() ,所以
,所以![]() ,即
,即![]() 成立.
成立.
(ⅱ)若![]() ,可得
,可得![]() 在
在![]() 上单调递增.
上单调递增.
因为![]() ,
,![]() ,所以存在
,所以存在![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时,![]() ,所以
,所以![]() 即
即![]() 在
在![]() 上单调递减,
上单调递减,
又因为![]() ,所以当
,所以当![]() 时,
时,![]() ,从而
,从而![]() 在
在![]() 上单调递减,
上单调递减,
而![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]() 不成立.
不成立.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】下列语句中正确的个数是( )
①![]() ,函数
,函数![]() 都不是偶函数;
都不是偶函数;
②命题“若![]() ,则
,则![]() ”的否命题是真命题;
”的否命题是真命题;
③若![]() 或
或![]() 为真,则
为真,则![]() ,非
,非![]() 均为真;
均为真;
④已知向量![]() ,则“
,则“![]() ”的充分不必要条件是“
”的充分不必要条件是“![]() 与
与![]() 夹角为锐角”.
夹角为锐角”.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查观众对某热播电视剧的喜爱程度,某电视台在甲、乙两地各随机抽取了![]() 名观众作问卷调查,得分统计结果如图所示.
名观众作问卷调查,得分统计结果如图所示.

(1)计算甲、乙两地被抽取的观众问卷的平均分与方差.
(2)若从甲地被抽取的![]() 名观众中再邀请
名观众中再邀请![]() 名进行深入调研,求这
名进行深入调研,求这![]() 名观众中恰有
名观众中恰有![]() 人的问卷调查成绩在
人的问卷调查成绩在![]() 分以上的概率.
分以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅游业作为一个第三产业,时间性和季节性非常强,每年11月份来临,全国各地就相继进入旅游淡季,很多旅游景区就变得门庭冷落.为改变这种局面,某旅游公司借助一自媒体平台做宣传推广,销售特惠旅游产品.该公司统计了活动刚推出一周内产品的销售数量,用![]() 表示活动推出的天数,用
表示活动推出的天数,用![]() 表示产品的销售数量(单位:百件),统计数据如下表所示.
表示产品的销售数量(单位:百件),统计数据如下表所示.
![]()

根据以上数据,绘制了如图所示的散点图,根据已有的函数知识,发现样本点分布在某一条指数型函数![]() 的周围.为求出该回归方程,相关人员确定的研究方案是:先用其中5个数据建立
的周围.为求出该回归方程,相关人员确定的研究方案是:先用其中5个数据建立![]() 关于
关于![]() 的回归方程,再用剩下的2组数据进行检验.试回答下列问题:
的回归方程,再用剩下的2组数据进行检验.试回答下列问题:
(1)现令![]() ,若选取的是
,若选取的是![]() 这5组数据,已知
这5组数据,已知![]() ,
,![]() ,请求出
,请求出![]() 关于
关于![]() 的线性回归方程(结果保留一位有效数字);
的线性回归方程(结果保留一位有效数字);
(2)若由回归方程得到的估计数据与选出的检验数据的误差均不超过![]() ,则认为得到的回归方程是可靠的,试问(1)中所得的回归方程是否可靠?
,则认为得到的回归方程是可靠的,试问(1)中所得的回归方程是否可靠?
参考公式及数据:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为 ,
, ![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有100名工人接受了生产1000台某产品的总任务,每台产品由9个甲型装置和3个乙型装置配套组成,每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置.设加工甲型装置的工人有x人,他们加工完甲型装置所需时间为![]() 小时,其余工人加工完乙型装置所需时间为
小时,其余工人加工完乙型装置所需时间为![]() 小时,则生产1000台某产品的总加工时间y是一个关于x的函数。
小时,则生产1000台某产品的总加工时间y是一个关于x的函数。
(1)求y关于x的函数解析式;
(2)如何分配工人才能使生产1000台某产品的总加工时间最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】山西省在2019年3月份的高三适应性考试中对数学成绩数据统计显示,全市10000名学生的成绩近似服从正态分布![]() ,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组
,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
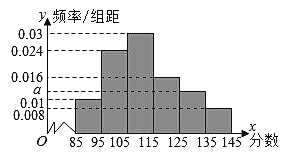
(1)求全市数学成绩在135分以上的人数;
(2)试由样本频率分布直方图佔计该校数学成绩的平均分数;
(3)若从这50名学生中成绩在125分(含125分)以上的同学中任意抽取3人,该3人在全市前13名的人数记为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() :
:![]() 的一个顶点重合,且这个顶点与椭圆
的一个顶点重合,且这个顶点与椭圆![]() 的两个焦点构成的三角形面积为
的两个焦点构成的三角形面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的上顶点为
的上顶点为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,连接
为坐标原点,连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市高三数学复习备考情况,该市教研机构组织了一次检测考试,并随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.

(1)根据频率分布直方图,估计该市此次检测理科数学的平均成绩![]() ;(精确到个位)
;(精确到个位)
(2)研究发现,本次检测的理科数学成绩![]() 近似服从正态分布
近似服从正态分布![]() (
(![]() ,
,![]() 约为
约为![]() ),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占
),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占![]() .
.
(ⅰ)估计本次检测成绩达到自主招生分数要求的理科数学成绩大约是多少分?(精确到个位)
(ⅱ)从该市高三理科学生中随机抽取![]() 人,记理科数学成绩能达到自主招生分数要求的人数为
人,记理科数学成绩能达到自主招生分数要求的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .(说明:
.(说明:![]() 表示
表示![]() 的概率.参考数据:
的概率.参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com