
分析 (1)根据题意,由公式an=Sn-Sn-1可得an=-4n+1,进而利用a1=s1计算可得a1的值,验证可得a1=-3符合计算出的an公式,即可得答案;
(2)由(1)求出an公式,可得等差数列{an}的公差d=-4<0,由等差数列的性质可得答案;
(3)根据题意,由等差数列的性质:a1+a3+a5+…+a25=13a13,由(1)求出通项公式计算可得答案.
解答 解:(1)根据题意,等差数列{an}的前n项和Sn=-2n2-n
则an=Sn-Sn-1=(-2n2-n)-[-2(n-1)2-(n-1)]=-4n+1,
n=1时,a1=s1=-3,也符合an=-4n+1,
故数列{an}的通项公式为an=-4n+1;
(2)由(1)可得,等差数列{an}的通项公式为an=-4n+1,
其公差d=-4<0,
则该数列为递减的等差数列;
(3)根据题意,由等差数列的性质:
a1+a3+a5+…+a25=13a13=13×(-4×13+1)=-663.
点评 本题考查等差数列的性质,涉及等差数列的通项公式,关键是正确求出该数列的通项公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
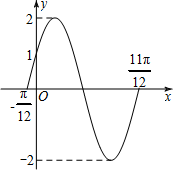 若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分图象如图所示.
若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11π | B. | 20π | C. | 23π | D. | 35π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
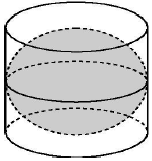 如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现.经计算球的体积等于圆柱体积的$\frac{2}{3}$倍.
如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现.经计算球的体积等于圆柱体积的$\frac{2}{3}$倍.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数,不是偶函数 | B. | 是偶函数,不是奇函数 | ||
| C. | 既是奇函数数,又是偶函数 | D. | 既不是奇函数,也不是偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com