[题目]已知函数.的部分图象如图所示．(Ⅰ)求函数的解析式,(Ⅱ)求函数的单调递增区间．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数，的部分图象如图所示．

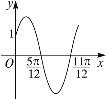
（Ⅰ）求函数的解析式；

（Ⅱ）求函数的单调递增区间．

【答案】（1）；（2）（）.

【解析】

试题（Ⅰ）根据图像与x轴的交点可求得，进而求得；然后根据函数图像过点(，0)可得，过点(0，1)可得A＝2，即可求得解析式f (x)＝2sin(2x＋)；（Ⅱ）用换元法即可求得g(x)的单调递增区间是(k∈Z).

试题解析：（Ⅰ）由题设图象知，周期，所以，

因为点(，0)在函数图象上，所以Asin(2×＋φ)＝0，即sin(＋φ)＝0.

又因为0＜φ＜，所以，从而＋φ＝π，即.

又点(0，1)在函数图象上，所以，得A＝2，

故函数f (x)的解析式为f (x)＝2sin(2x＋)．

（Ⅱ）由，

得，k∈Z，

所以函数g(x)的单调递增区间是(k∈Z).

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数=+，其中a>0且a≠1。

（1）求函数的定义域；

（2）若函数有最小值而无最大值，求的单调增区间。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】等差数列{an}的前n项和为Sn ．已知a1=10，a2为整数，且Sn≤S4 ．
（1）求{an}的通项公式；
（2）设bn= ，求数列{bn}的前n项和Tn ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，四棱锥P﹣ABCD，底面是以O为中心的菱形，PO⊥底面ABCD，AB=2，∠BAD= ，M为BC上的一点，且BM= ，MP⊥AP．

（1）求PO的长；
（2）求二面角A﹣PM﹣C的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，设椭圆（a＞b＞0）的左、右焦点分别为F1 ， F2 ，点D在椭圆上．DF1⊥F1F2 ， =2 ，△DF1F2的面积为．

（1）求椭圆的标准方程；
（2）设圆心在y轴上的圆与椭圆在x轴的上方有两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点，求圆的半径．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】记max{x，y}= ，min{x，y}= ，设，为平面向量，则（）
A.min{| + |，| ﹣ |}≤min{| |，| |}
B.min{| + |，| ﹣ |}≥min{| |，| |}
C.max{| + |2 ， | ﹣ |2}≤| |2+| |2
D.max{| + |2 ， | ﹣ |2}≥| |2+| |2

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设数列{an}的前n项和为Sn．已知S2=4,an+1=2Sn+1,n∈N*．

(1)求通项公式an;

(2)求数列{|an-n-2|}的前n项和．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】九章算术是我国古代著名数学经典其中对勾股定理的论述比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深一寸，锯道长一尺问这块圆柱形木料的直径是多少？长为1丈的圆柱形木材部分镶嵌在墙体中，截面图如图所示阴影部分为镶嵌在墙体内的部分已知弦尺，弓形高寸，估算该木材镶嵌在墙中的体积约为( )(注：1丈尺寸，，)