
设函数f(x)定义在(0,+∞)上,f(1)=0,导函数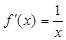 ,
,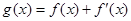 .
.
(1)求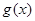 的单调区间和最小值;
的单调区间和最小值;
(2)讨论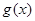 与
与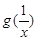 的大小关系;
的大小关系;
(3)是否存在x0>0,使得|g(x)﹣g(x0)|<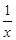 对任意x>0成立?若存在,求出x0的取值范围;若不存在请说明理由.
对任意x>0成立?若存在,求出x0的取值范围;若不存在请说明理由.
(1)g(x)的单调递减区间是(0,1),单调递增区间是(1,+∞),最小值为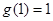 ;(2)当0<x<1时,
;(2)当0<x<1时,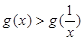 ;当x>1时,
;当x>1时,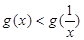 ;(3)满足条件的x0不存在.证明详见解析.
;(3)满足条件的x0不存在.证明详见解析.
解析试题分析:(1)由题设得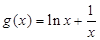 ,求导,根据导数的符号即可确定g(x)的单调区间,进而求出其最小值;(2)为了确定
,求导,根据导数的符号即可确定g(x)的单调区间,进而求出其最小值;(2)为了确定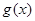 与
与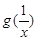 的大小关系,便作差判断其符号.设
的大小关系,便作差判断其符号.设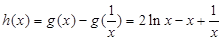 ,则
,则 ,因此
,因此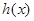 在
在 内单调递减.接下来就确定函数
内单调递减.接下来就确定函数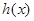 的零点.易知h(1)=0,即
的零点.易知h(1)=0,即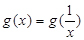 ;所以当0<x<1,时,h(x)>h(1)=0,即
;所以当0<x<1,时,h(x)>h(1)=0,即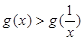 ,当x>1,时,h(x)<h(1)=0,即
,当x>1,时,h(x)<h(1)=0,即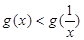 ;(3)根据(1)题的结果可作出
;(3)根据(1)题的结果可作出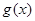 的大致图象;再作出
的大致图象;再作出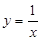 的图象,结合图象可看出,不论
的图象,结合图象可看出,不论 取多少,当
取多少,当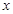 的值充分大时,必有
的值充分大时,必有 ,所以满足条件的x0不存在.接下来就是想方设法找出一个
,所以满足条件的x0不存在.接下来就是想方设法找出一个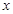 ,使得
,使得 .为了更容易地找出这样的
.为了更容易地找出这样的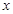 ,我们将
,我们将 变形为
变形为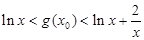 ,对左边的不等式
,对左边的不等式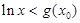 ,易看出当
,易看出当 时便不成立.从而问题得证.
时便不成立.从而问题得证.
试题解析:(1)由题设易知 ,
,
∴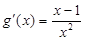 ,令
,令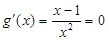 ,得
,得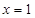 ,
,
当x∈(0,1)时,g′(x)<0,故g(x)的单调递减区间是(0,1),
当x∈(1,+∞)时,g′(x)>0,故g(x)的单调递增区间是(1,+∞),
因此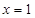 是
是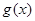 的唯一极值点,且为极小值点,从而是最小值点,
的唯一极值点,且为极小值点,从而是最小值点,
∴最小值为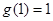 ;
;
(2)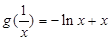 ,
,
设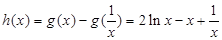 ,
,
则 ,
,
当x=1时,h(1)=0,即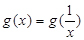 ,
,
当x∈(0,1)∪(1,+∞)时,h′(x)<0,h′(1)=0,
因此,h(x)在 内单调递减,
内单调递减,
当0<x<1,时,h(x)>h(1)=0,即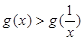 ,
,
当x>1,时,h(x)<h(1)=0,即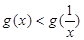 ,
,
(3)满足条件的x0不存在.证明如下:假设存在x0>0,
使 成立,即对任意x>0,
成立,即对任意x>0,
有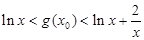 ,(*)
,(*)
但对上述x0,取 时,
时,
有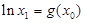 ,这与(*)左边不等式矛盾,
,这与(*)左边不等式矛盾,
因此,不存在x0>0,使 成立.
成立.
考点:1、导数及其应用;2、导数与不等式.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:解答题
设函数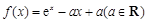 ,其图象与
,其图象与 轴交于
轴交于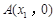 ,
, 两点,且x1<x2.
两点,且x1<x2.
(1)求 的取值范围;
的取值范围;
(2)证明: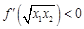 (
( 为函数
为函数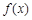 的导函数);
的导函数);
(3)设点C在函数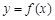 的图象上,且△ABC为等腰直角三角形,记
的图象上,且△ABC为等腰直角三角形,记 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 其中
其中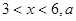 为常数。己知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。己知销售价格为5元/千克时,每日可售出该商品11千克。
(1)求 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com