
【题目】已知函数f(x)![]() x+alnx.
x+alnx.
(1)求f(x)在(1,f(1))处的切线方程(用含a的式子表示)
(2)讨论f(x)的单调性;
(3)若f(x)存在两个极值点x1,x2,证明:![]() .
.
【答案】(1)y=(﹣2+a)x+2﹣a.(2)见解析(3)见解析
【解析】
(1)求出切点坐标,根据导函数求出切线斜率,即可得到切线方程;
(2)求出导函数,对g(x)=﹣x2+ax﹣1,进行分类讨论即可得到原函数单调性;
(3)结合(2)将问题转为证明![]() 1,根据韦达定理转化为考虑h(x)=2lnx﹣x
1,根据韦达定理转化为考虑h(x)=2lnx﹣x![]() 的单调性比较大小即可得证.
的单调性比较大小即可得证.
(1)∵f(x)![]() x+alnx(x>0)
x+alnx(x>0)
∴f′(x)![]() (x>0)
(x>0)
∴当x=1时,f(1)=0,f′(1)=﹣2+a,
设切线方程为y=(﹣2+a)x+b,代入(1,0),得b=2﹣a,
∴f(x)在(1,f(1))处的切线方程为y=(﹣2+a)x+2﹣a.
(2)函数的定义域为(0,+∞),
函数的导数f′(x)![]() ,
,
设g(x)=﹣x2+ax﹣1,注意到g(0)=﹣1,
①当a≤0时,g(x)<0恒成立,即f′(x)<0恒成立,此时函数f(x)在(0,+∞)上是减函数;
②当a>0时,判别式△=a2﹣4,
(i)当0<a≤2时,△≤0,即g(x)≤0,即f′(x)≤0恒成立,此时函数f(x)在(0,+∞)上是减函数;
(ii)当a>2时,令f′(x)>0,得:![]() x
x![]() ;
;
令f′(x)<0,得:0<x![]() 或x
或x![]() ;
;
∴当a>2时,f(x)在区间(![]() ,
,![]() )单调递增,在(0,
)单调递增,在(0,![]() ),(
),(![]() ,+∞)单调递减;
,+∞)单调递减;
综上所述,综上当a≤2时,f(x)在(0,+∞)上是减函数,
当a>2时,在(0,![]() ),(
),(![]() ,+∞)上是减函数,
,+∞)上是减函数,
在区间(![]() ,
,![]() )上是增函数.
)上是增函数.
(3)由(2)知a>2,0<x1<1<x2,x1x2=1,
则f(x1)﹣f(x2)![]() x1+alnx1﹣[
x1+alnx1﹣[![]() x2+alnx2]
x2+alnx2]
=(x2﹣x1)(1![]() )+a(lnx1﹣lnx2)
)+a(lnx1﹣lnx2)
=2(x2﹣x1)+a(lnx1﹣lnx2),
则![]() 2
2![]() ,
,
则问题转为证明![]() 1即可,
1即可,
即证明lnx1﹣lnx2>x1﹣x2,
则lnx1﹣ln![]() x1
x1![]() ,
,
即lnx1+lnx1>x1![]() ,
,
即证2lnx1>x1![]() 在(0,1)上恒成立,
在(0,1)上恒成立,
设h(x)=2lnx﹣x![]() ,(0<x<1),其中h(1)=0,
,(0<x<1),其中h(1)=0,
求导得h′(x)![]() 1
1![]() 0,
0,
则h(x)在(0,1)上单调递减,
∴h(x)>h(1),即2lnx﹣x![]() 0,
0,
故2lnx>x![]() ,
,
则![]() a﹣2成立.
a﹣2成立.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:
【题目】如图,设抛物线![]() 的焦点为F,准线为l,过准线l上一点
的焦点为F,准线为l,过准线l上一点![]() 且斜率为k的直线
且斜率为k的直线![]() 交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.
交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.
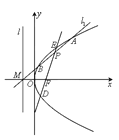
(1)求抛物线C的方程及k的取值范围;
(2)是否存在k值,使点P是线段DE的中点?若存在,求出k值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某包子店每天早晨会提前做好一定量的包子,以保证当天及时供应,该包子店记录了60天包子的日需求量![]() (单位:个,
(单位:个,![]() ).按
).按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,整理得到如图所示的频率分布直方图,图中
分组,整理得到如图所示的频率分布直方图,图中![]() .
.
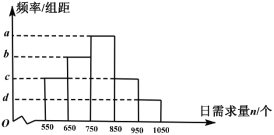
(1)求包子日需求量平均数的估计值(每组以中点值作为代表);
(2)若包子店想保证至少![]() 的天数能够足量供应,则每天至少要做多少个包子?
的天数能够足量供应,则每天至少要做多少个包子?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
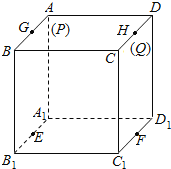
A.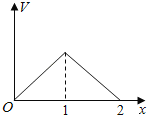 B.
B.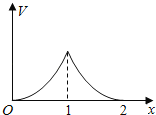
C.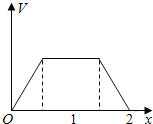 D.
D.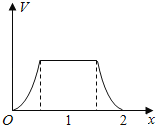
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个水轮的半径为![]() ,水轮轴心
,水轮轴心![]() 距离水面的高度为
距离水面的高度为![]() ,已知水轮按逆时针匀速转动,每分钟转动
,已知水轮按逆时针匀速转动,每分钟转动![]() 圈,当水轮上点
圈,当水轮上点![]() 从水中浮现时的起始(图中点
从水中浮现时的起始(图中点![]() )开始计时,记
)开始计时,记![]() 为点
为点![]() 距离水面的高度关于时间
距离水面的高度关于时间![]() 的函数,则下列结论正确的是( )
的函数,则下列结论正确的是( )
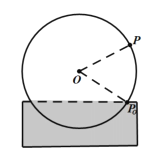
A.![]()
B.![]()
C.若![]() ,则
,则![]()
D.不论![]() 为何值,
为何值,![]() 是定值
是定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个统计案例如下:
①为了探究患慢性支气管炎与吸烟关系,调查了339名50岁以上的人,调查结果如表:
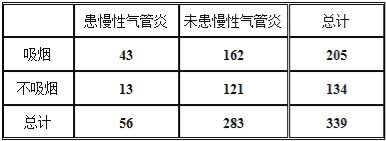
②为了解某地母亲与女儿身高的关系,随机测得10对母女的身高如下表: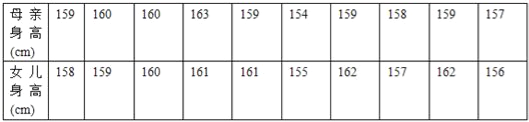
则对这些数据的处理所应用的统计方法是( )
A.①回归分析②取平均值
B.①独立性检验②回归分析
C.①回归分析②独立性检验
D.①独立性检验②取平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三角形的边长为不相等的整数,且最大边长为n,这些三角形的个数为an.
(1)求数列{an}的通项公式;
(2)在1,2,…,100中任取三个不同的整数,求它们可以是一个三角形的三条边长的概率.
附:1+22+32+…+n2![]() ;1+23+33+…+n3
;1+23+33+…+n3![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com