
| π |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
|
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| S |
| (vt)2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |




科目:高中数学 来源: 题型:
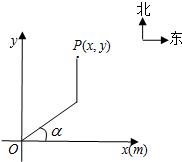 根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α(0≤α≤
根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α(0≤α≤| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
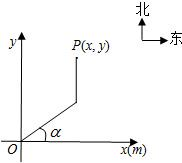 根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α(0≤α≤
根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α(0≤α≤| π |
| 2 |
| A、100π |
| B、100π-200 |
| C、400-100π |
| D、200 |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省南通市启东中学高三数学考前辅导材料(1)(解析版) 题型:解答题
 )内的变量)方向或正北方向行走,且方向改变的时间不定.记机器人行走t(s)时的可能落点P的区域为Ω,则Ω的面积与(vt)2的比值为 .
)内的变量)方向或正北方向行走,且方向改变的时间不定.记机器人行走t(s)时的可能落点P的区域为Ω,则Ω的面积与(vt)2的比值为 .查看答案和解析>>
科目:高中数学 来源:2009年北京市西城区高考数学二模试卷(理科)(解析版) 题型:选择题
 )方向行走一段时间后,再向正北方向行走一段时间,但α的大小以及何时改变方向不定.如图.假定机器人行走速度为10米/分钟,设机器人行走2分钟时的可能落点区域为S,则S的面积(单位:平方米)等于( )
)方向行走一段时间后,再向正北方向行走一段时间,但α的大小以及何时改变方向不定.如图.假定机器人行走速度为10米/分钟,设机器人行走2分钟时的可能落点区域为S,则S的面积(单位:平方米)等于( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com