考点:等比关系的确定,等差数列的性质
专题:等差数列与等比数列
分析:(1)由对于任意的正整数m,n,恒有(n-m)S
n+m=(n+m)(S
n-S
m).令m=1,n=2,可得S
3=3a
2,进而得到答案;
(2)令m=1,则(n-1)S
n+1=(n+1)(S
n-S
1),可得a
n+3-a
n+2=a
n+2-a
n+1,结合(1)中结论得到a
2-a
1=a
3-a
2也成立,则a
n+2-a
n+1=a
n+1-a
n,即数列{a
n}为等差数列;
(3)数列{a
n}的公差不为零且a
p,a
q,a
r,a
s成等比数列,可得
==,即q-p=r-q=s-r≠0,即q-p,r-q,s-r成等比数列,且公比不为1.
解答:
(1)解:∵对于任意的正整数m,n,恒有(n-m)S
n+m=(n+m)(S
n-S
m).
令m=1,n=2,则S
3=3a
2,
∴
=3(2)证明:令m=1,则(n-1)S
n+1=(n+1)(S
n-S
1),
∴nS
n+2=(n+2)(S
n+1-S
1),
∴nS
n+2-(n-1)S
n+1=(n+2)(S
n+1-S
1)-(n+1)(S
n-S
1),
∴na
n+2=(n+1)a
n+1-S
1,∴(n+1)a
n+3=(n+2)a
n+2-S
1,
∴(n+1)a
n+3-na
n+2=(n+2)a
n+2-(n+1)a
n+1,
∴a
n+3-a
n+2=a
n+2-a
n+1,又∵S
3=2a
2,
∴a
2-a
1=a
3-a
2,
∴a
n+2-a
n+1=a
n+1-a
n,
∴数列{a
n}为等差数列
(3)证明:∵a
1≠a
2,
∴数列{a
n}的公差不为零
∵a
p,a
q,a
r,a
s成等比数列,
∴
==记公比为x,则x≠1,且x
q-p=x
r-q=x
s-r∴q-p=r-q=s-r≠0
∴q-p,r-q,s-r成等比数列,且公比不为1.
点评:本题考查的知识点是等差数列的性质和定义,等比数列的性质和定义,是等差数列与等比数列的综合应用,难度中档.



 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案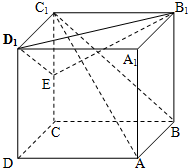 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结BC1,过点B1作BC1的垂线交CC1于E.
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结BC1,过点B1作BC1的垂线交CC1于E.