
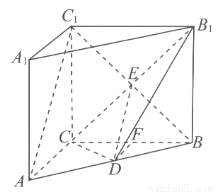
如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.

(1)求证:AC1∥平面CDB1;
(2)求四面体B1C1CD的体积.
(1)证明过程详见试题解析;(2)三棱锥D-B1C1C的体积为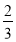 .
.
【解析】
试题分析:(1)连接BC1,设BC1与B1C的交点为E,连接DE,证得DE∥AC1;由线面平行的判定定理即可证明AC1∥平面CDB1;(2)在平面ABC内作DF⊥BC于点F,可以证明DF是三棱锥D-CC1B1的高,再由锥体体积公式即可求解.
试题解析:
(1)证明:连结BC1,设BC1与B1C的交点为E,连结DE.
∵三棱柱ABC-A1B1C1,CC1⊥底面ABC,CC1=BC=2,
∴四边形BCC1B1为正方形. ∴E为BC1中点.
∵D是AB的中点, ∴DE∥AC1.
∵DE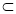 平面CDB1,AC1
平面CDB1,AC1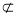 平面CDB1,
平面CDB1,
∴AC1∥平面CDB1. 4分
(2)在平面ABC内作DF⊥BC于点F,
∵CC1⊥平面ACB , DF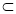 平面ACB,
平面ACB,
∴CC1⊥DF.
∵BC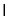 CC1=C
CC1=C
∴DF⊥平面BCC1B1.
∴DF是三棱锥D-CC1B1的高,
∵AC=BC=CC1=2
∴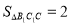 DF=1.
DF=1.
∴四面体B1C1CD的体积为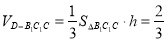 . 9分
. 9分
考点:线面平行的判定定理、空间几何体的体积.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源:2015届北京海淀区高二上学期期末考试理科数学试卷(解析版) 题型:选择题
已知命题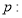 椭圆的离心率
椭圆的离心率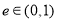 ,命题
,命题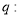 与抛物线只有一个公共点的直线是此抛物线的切线,那么( )
与抛物线只有一个公共点的直线是此抛物线的切线,那么( )
(A) 是真命题 (B)
是真命题 (B) 是真命题
是真命题
(C) 是真命题 (D)
是真命题 (D)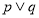 是假命题
是假命题
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二第一学期期末理科数学试卷(解析版) 题型:选择题
“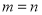 ”是“方程
”是“方程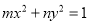 表示圆”的 ( )
表示圆”的 ( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二第一学期期末文科数学试卷(解析版) 题型:选择题
已知椭圆 ,
, 为坐标原点.若
为坐标原点.若 为椭圆上一点,且在
为椭圆上一点,且在 轴右侧,
轴右侧, 为
为 轴上一点,
轴上一点, ,则点
,则点 横坐标的最小值为( )
横坐标的最小值为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试理数学试卷(解析版) 题型:选择题
一组数据的方差是s2,将这组数据中的每一个数据都乘以2,所得到的一组数据的方差是
A. 2s2 B. 4s2 C. 8s2 D. 16s2
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试文数学试卷(解析版) 题型:选择题
甲、乙、丙三名毕业生参加某公司人力资源部安排的面试,三人依次进行,每次一人,其中甲、乙两人相邻的概率为
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com