
将一个三位数的三个数字顺序颠倒,将所得到的数和原数相加,若和中没有一个数字是偶数,则称这个数是奇和数。那么,所有的三位数中,奇和数有( )
| A.80 | B.100 | C.120 | D.160 |
B
解析试题分析:设这个3位数为100a+10b+c.则顺序颠倒后为100c+10b+a.则两个数相加为101a+20b+101c.根据“奇和数”的定义,分别讨论a,b,c的取值.从而得出答案.
由分析得两个数相加为101a+20b+101c=100(a+c)+20b+(a+c)
如果此数的每一位都为奇数.那么a+c必为奇数,由于20b定为偶数,所以如果让十位数为奇数,那么a+c必须大于10,又当b≥5时,百位上进1,那么百位必为偶数,
所以b<5.b可取0,1,2,3,4,由于a+c为奇数,且a+c>10
所以满足条件的有:
当a=2时,c=9.当a=3时,c=8.当a=4时,c=7,9.
当a=5时,c=6,8.当a=6时,c=5,7,9.当a=7时,c=4,6,8.
当a=8时,c=3,5,7,9.当a=9时,c=2,4,6,8.
共有20种情况,由于b可取0,1,2,3,4.
故20×5=100,故选B.
考点:排列组合的运用。
点评:本题考查了整数的奇偶性问题,解决本题的关键是分情况讨论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:单选题
有11名学生,其中女生3名,男生8名,从中选出5名学生组成代表队,要求至少有1名女生参加,则不同的选派方法种数是 ( )
| A.406 | B.560 | C.462 | D.154 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
反复抛掷一枚质地均匀的骰子,每一次抛掷后都记录下朝上一面的点数,当记录有三个不同点数时即停止抛掷,则抛掷五次后恰好停止抛掷的不同记录结果总数是( )
A.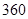 种 种 | B.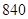 种 种 | C.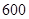 种 种 | D. 种 种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com