
已知函数 。
。
(1)求函数 的定义域;
的定义域;
(2)判断函数 的奇偶性;
的奇偶性;
(3)讨论函数 的单调性(不用证明)。
的单调性(不用证明)。
(1) ;(2)奇函数;(3)
;(2)奇函数;(3)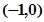 减函数 ;
减函数 ; 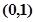 减函数;
减函数;
解析试题分析:(1)由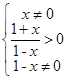 得:
得: ,所以函数的定义域为
,所以函数的定义域为 。
。
(2)由(1)知,函数的定义域为 ,关于原点对称,
,关于原点对称,
又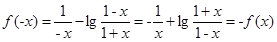 ,所以f(x) 是奇函数。
,所以f(x) 是奇函数。
(3)令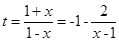 ,则函数t在(0,1)上是单调递增的,又y=-lgt在(0,1)上是单调递减的,所以y=
,则函数t在(0,1)上是单调递增的,又y=-lgt在(0,1)上是单调递减的,所以y= 在(0,1)上是单调递减的,所以
在(0,1)上是单调递减的,所以 在(0,1)上是单调递减的,,又因为f(x)是奇函数,所以f(x) 在(-1,0)上是单调递减的。
在(0,1)上是单调递减的,,又因为f(x)是奇函数,所以f(x) 在(-1,0)上是单调递减的。
考点:本题考查函数的定义域;函数的奇偶性;函数的单调性;分式不等式的解法;复合函数的单调性。
点评:本题主要考查了奇偶性与单调性的综合,同时也考查了函数的定义域,复合函数等。熟练掌握基本初等函数的性质和复合函数单调性的判断是解答本题的关键.


科目:高中数学 来源: 题型:解答题
(本小题满分15分)已知函数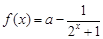 ,
,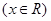 .
.
(1)用定义证明:不论 为何实数
为何实数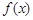 在
在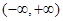 上为增函数;
上为增函数;
(2)若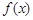 为奇函数,求
为奇函数,求 的值;
的值;
(3)在(2)的条件下,求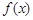 在区间[1,5]上的最小值.
在区间[1,5]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知f (x)=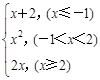 .
.
(1)求函数f (x)的值域.
(2)若f (t)=3,求t的值.
(3)用单调性定义证明在[2,+∞)上单调递增.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 已知方程
 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求:
(Ⅰ)若方程 的根为一正一负,则求实数
的根为一正一负,则求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 的两根都在
的两根都在 内,则求实数
内,则求实数 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com