
【题目】在如图所示的空间几何体中,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上. 
(1)求证:DE∥平面ABC;
(2)求二面角E﹣BC﹣A的余弦值.
【答案】
(1)证明:由题意知,△ABC,△ACD都是边长为2的等边三角形,
取AC中点O,连接BO,DO,
则BO⊥AC,DO⊥AC∵平面ACD⊥平面ABC
∴DO⊥平面ABC,作EF⊥平面ABC,
那么EF∥DO,根据题意,点F落在BO上,
∴∠EBF=60°,∴EF=DO= ![]() ,
,
所以四边形DEFO是平行四边形,DE∥OF;
∵DE平面ABC,OF平面ABC,∴DE∥平面ABC
(2)解:方法一:作FG⊥BC,垂足为G,连接FG;

∵EF⊥平面ABC,根据三垂线定理可知,EG⊥BC,
∴∠EGF就是二面角E﹣BC﹣A的平面角,
BF= ![]() =
= ![]() ,
,
∵FG=BFsin∠FBG= ![]() ,EF=
,EF= ![]() ,
,
∴EG= ![]() =
= ![]() ,
,
∴cos∠EGF= ![]() =
= ![]() ,
,
即二面角E﹣BC﹣A的余弦值为 ![]() .
.
方法二:建立如图所示的空间直角坐标系O﹣xyz,

可求得平面ABC的一个法向量为 ![]() ,
,
平面BCE的一个法向量为 ![]()
所以  =
= ![]()
又由图知,所求二面角的平面角是锐角,二面角E﹣BC﹣A的余弦值为 ![]() .
.
【解析】(1)证明线面平行,需要证明直线平行面内的一条直线即可.(2)法一:利用三垂线定理作出二面角的平面角即可求解.法二:建立空间直角坐标系,利用向量法求解
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】某医药研究所开发一种新药, 成年人按规定的剂量服用后, 每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间关系满足如图所示的曲线.
(小时)之间关系满足如图所示的曲线.
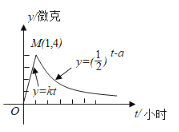
(1)写出![]() 关于
关于![]() 的函数关系式:
的函数关系式:![]() ;
;
(2)据进一步测定: 每毫升血液中的含药量不少于![]() 微克时, 治疗疾病有效. 求服药一次后治疗疾病有效的时间.
微克时, 治疗疾病有效. 求服药一次后治疗疾病有效的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)=ex+ae﹣x为偶函数,则f(x﹣1)< ![]() 的解集为( )
的解集为( )
A.(2,+∞)
B.(0,2)
C.(﹣∞,2)
D.(﹣∞,0)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1,F2分别是椭圆C:![]() (a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为![]() ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是 ![]() .
.
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为ξ.求ξ的分布列及数学期望E(ξ).( 结果用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2
(t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2 ![]() cosθ.
cosθ.
(1)求C2与C3交点的直角坐标;
(2)若C2与C1相交于点A,C3与C1相交于点B,求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设 ![]() =m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( )
=m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( ) 
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上一点C,⊙O的半径为3,△AOB是等腰三角形,且C是AB中点,⊙O交直线OB于E、D. 
(1)证明:直线AB与⊙O相切;
(2)若∠CED的正切值为 ![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com