
 平面PCB;(2)求二面角C—PA—B的大小.
平面PCB;(2)求二面角C—PA—B的大小.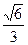
 平面ABC,
平面ABC,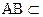 平面ABC,
平面ABC, AB
AB
|
 平面PAB,
平面PAB,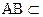 平面PAB,∴CD
平面PAB,∴CD AB又
AB又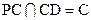 ,
, 平面PCB.…6分
平面PCB.…6分 PA,CE=
PA,CE=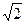 .
. 平面PAB,
平面PAB, PA.
PA.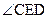 为二面角C-PA-B的平面角.
为二面角C-PA-B的平面角. 平面PCB,又∵AB⊥BC,又AB=BC,AC=2,可求得BC=
平面PCB,又∵AB⊥BC,又AB=BC,AC=2,可求得BC=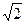 .
.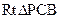 中,PB=
中,PB=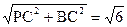 ,
,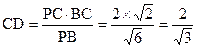 .
.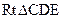 中, sin∠CED=
中, sin∠CED=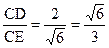 .
.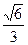 .…………14分
.…………14分
|
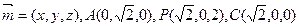
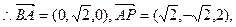
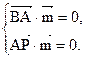 即
即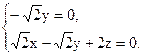

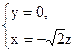
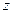 =" -1, " 得
=" -1, " 得 = (
= (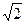 ,0,-1)
,0,-1)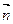 =(
=(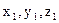 ).
).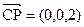 ,
,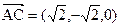 ,
,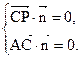 即
即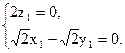
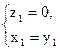 令
令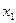 ="1, " 得
="1, " 得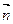 = (1,1,0).
= (1,1,0).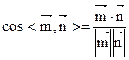 =
=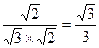
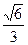


科目:高中数学 来源:不详 题型:填空题
 ,BB1=2,∠ABC=90°,E、F分为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度是________.
,BB1=2,∠ABC=90°,E、F分为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度是________. 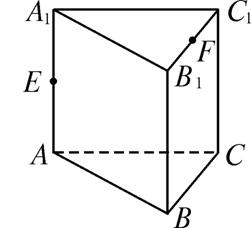
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 X∥Y”为真命题的是_________(填序号)
X∥Y”为真命题的是_________(填序号)
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com