
| A. | ①② | B. | ①③④ | C. | ①③ | D. | ②④ |
分析 ①由题意得到A、B的互推关系,结合逆否命题的真假判断;
②由x=-2时,x2=4说明命题错误;
③由正弦定理知$\frac{a}{sinA}=\frac{b}{sinB}$,由sinA>sinB,知a>b,所以A>B,反之亦然,故可得结论;
④由所给的方程意义是两数绝对值的和等于两数和的绝对值,此两数的符号一定相同或有一数为0判断.
解答 解:①∵A是B的必要不充分条件,∴由B可得A,但由A不能得B,
∴由¬A可得¬B,但由¬B不能得¬A,则?B也是?A的必要不充分条件,①正确;
②当x=-2时,x2=4,∴“x≠2”不是“x2≠4”的充分条件,②错误;
③在△ABC中,由正弦定理知$\frac{a}{sinA}=\frac{b}{sinB}$=2R,
∵sinA>sinB,∴a>b,则A>B.
反之,∵A>B,∴a>b,
∵a=2RsinA,b=2RsinB,∴sinA>sinB
“sinA>sinB”是“A>B”的充要条件,③正确;
④由|a+b|=|a|+|b|,得a2+2ab+b2=a2+2|ab|+b2,即ab=|ab|,故ab≥0,又ab≥0,则a,b同号或有一数为0,故有|a+b|=|a|+|b|,
∴若a、b是实数,则“|a+b|=|a|+|b|”的充要条件是“ab≥0”,④正确.
故选:B.
点评 本题考查命题的真假判断与应用,考查充要条件的判定方法,对本问题的分析分为充分性与必要性两个方面,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 各正三角形内一点 | B. | 各正三角形的某高线上的点 | ||
| C. | 各正三角形的中心 | D. | 各正三角形外的某点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
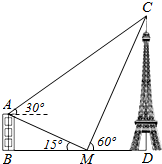 如图,一栋建筑物AB的高为(30-10$\sqrt{3}$)m,在该建筑物的正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为( )
如图,一栋建筑物AB的高为(30-10$\sqrt{3}$)m,在该建筑物的正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为( )| A. | 30m | B. | 60m | C. | 30$\sqrt{3}$m | D. | 40$\sqrt{3}$m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com