
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)对于任意的![]() ,
,![]() 的图象恒在
的图象恒在![]() 图象的上方,求实数a的取值菹围.
图象的上方,求实数a的取值菹围.
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形ABEF中,![]() ,
,![]() ,矩形ABEF可沿AB任意翻折.
,矩形ABEF可沿AB任意翻折.

(1)求证:当点F,A,D不共线时,线段MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,线段MN总与线段FD平行”这个结论正确吗?如果正确,请证明;如果不正确,请说明能否改变个别已知条件使上述结论成立,并给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
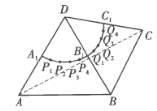
【题目】如图,正四面体![]() 的各棱长均为2,
的各棱长均为2,![]() 、
、![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 、
、![]() 的中点,以
的中点,以![]() 为圆心、1为半径,分别在面
为圆心、1为半径,分别在面![]() 、面
、面![]() 内作弧
内作弧![]() ,并将两弧各分成五等份,分点顺次为
,并将两弧各分成五等份,分点顺次为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 以及
以及![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .一只甲虫欲从点
.一只甲虫欲从点![]() 出发,沿四面体表面爬行至点
出发,沿四面体表面爬行至点![]() ,则其爬行的最短距离为___________。
,则其爬行的最短距离为___________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园内有一块以![]() 为圆心半径为
为圆心半径为![]() 米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形
米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形![]() 区域,其中两个端点
区域,其中两个端点![]() ,
,![]() 分别在圆周上;观众席为梯形
分别在圆周上;观众席为梯形![]() 内切在圆
内切在圆![]() 外的区域,其中
外的区域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在点
在点![]() 的同侧.为保证视听效果,要求观众席内每一个观众到舞台
的同侧.为保证视听效果,要求观众席内每一个观众到舞台![]() 处的距离都不超过
处的距离都不超过![]() 米.设
米.设![]() ,
,![]() .问:对于任意
.问:对于任意![]() ,上述设计方案是否均能符合要求?
,上述设计方案是否均能符合要求?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给图中A,B,C,D,E,F六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有4种颜色可供选择,则共有___种不同的染色方案.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() .
.
(1)若直线![]() 过点
过点![]() 且到圆心
且到圆心![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 的斜率为负),当
的斜率为负),当![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com