
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 的一条切线经过点
的一条切线经过点![]() ,求这条切线的方程.
,求这条切线的方程.
(2)若关于![]() 的方程
的方程![]() 有两个不相等的实数根x1,x2。
有两个不相等的实数根x1,x2。
①求实数a的取值范围;
②证明: ![]() .
.
【答案】(1)![]() 或
或![]() .(2)①
.(2)①![]() ②见解析
②见解析
【解析】试题分析:(1)先设切线点斜式方程,再与二次函数联立方程组,利用判别式为零得斜率(2)①先求函数导数,分类讨论导函数零点,单调函数至多一个零点,所以函数不单调,再依次讨论对应单调区间上有零点满足的条件②构造函数![]() ,
, ![]() ,利用导数易得函数单调递增,即得结论
,利用导数易得函数单调递增,即得结论
试题解析:解:(1)解法一 设经过点![]() 的切线与曲线
的切线与曲线![]() 相切于点
相切于点![]() ,
,
由![]() 得
得![]() ,
,
所以该切线方程为![]() ,
,
因为该切线经过![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以切线方程为![]() 或
或![]() .
.
解法二 由题意得曲线![]() 的切线的斜率一定存在,
的切线的斜率一定存在,
设所求的切线方程为![]() ,
,
由 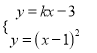 ,得
,得![]() ,
,
因为切线与抛物线相切,
所以![]() ,解得
,解得![]() ,
,
所以所求的切线方程为![]() 或
或![]() .
.
(2)①由![]() ,得
,得![]() .
.
设![]() ,
,
则![]() ,
,
由题意得函数![]() 恰好有两个零点.
恰好有两个零点.
(i)当![]() ,则
,则![]() ,
,
![]() 只有一个零点1.
只有一个零点1.
(ii)当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
即![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
而![]() ,
,
所以![]() 在
在![]() 上有唯一零点,且该零点在
上有唯一零点,且该零点在![]() 上.
上.
取![]() 且
且![]() ,
,
则![]()
所以![]() 在
在![]() 上有唯一零点,且该零点在
上有唯一零点,且该零点在![]() 上,
上,
所以![]() 恰好有两个零点.
恰好有两个零点.
(iii)当![]() 时,由
时,由![]() 得
得![]() ,
,
若![]() ,
, ![]() ,
,
所以![]() 在
在![]() 上至多有一个零点.
上至多有一个零点.
若![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,所以
,所以![]() 在
在![]() 上至多有一个零点.
上至多有一个零点.
当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上为减函数,
上为减函数,
又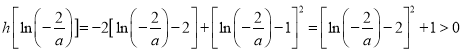 ,
,
所以h(x)在![]() 上无零点.
上无零点.
若![]() ,则
,则![]() ,
,
又当![]() 时,
时, ![]() ,
,
所以![]() 不存在零点.
不存在零点.
![]() 在
在![]() 上无零点
上无零点
故当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
因此![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
又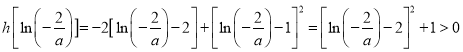 。
。
所以![]() 在
在![]() 无零点,在
无零点,在![]() 至多有一个零点.
至多有一个零点.
综上, ![]() 的取值范围为
的取值范围为![]() .
.
②不妨设![]() ,
,
由①知![]() ,
, ![]() ,且
,且![]() ,
, ![]() 在
在![]() 单调递减,
单调递减,
所以![]() 等价于
等价于![]() ,即
,即![]() .
.
由于![]() ,
,
且![]() ,
,
所以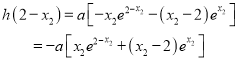 .
.
设![]() ,
,
则![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() .
.
而![]() ,故当
,故当![]() 时,
时, ![]() .
.
从而![]() ,故
,故![]() .
.


科目:高中数学 来源: 题型:
【题目】2016年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速![]() 分成六段:
分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
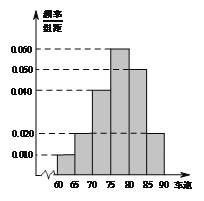
(I)某调查公司在采样中,用到的是什么抽样方法?
(II)求这40辆小型车辆车速的众数、中位数及平均数的估计值;
(III)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆至少有一辆的概率.
的车辆至少有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
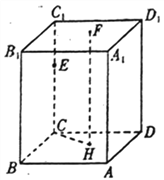
【题目】如图所示,直平行六面体![]() 中,
中,![]() 为棱
为棱![]() 上任意一点,
上任意一点,![]() 为底面
为底面![]() (除
(除![]() 外)上一点,已知
外)上一点,已知![]() 在底面
在底面![]() 上的射影为
上的射影为![]() ,若再增加一个条件,就能得到
,若再增加一个条件,就能得到![]() ,现给出以下条件:
,现给出以下条件:
①![]() ;②
;②![]() 在
在![]() 上;③
上;③![]() 平面
平面![]() ;④直线
;④直线![]() 和
和![]() 在平面
在平面![]() 的射影为同一条直线.其中一定能成为增加条件的是__________.(把你认为正确的都填上)
的射影为同一条直线.其中一定能成为增加条件的是__________.(把你认为正确的都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质监部门从某超市销售的甲、乙两种食用油中分别各随机抽取100桶检测某项质量指标,由检测结果得到如下的频率分布直方图:
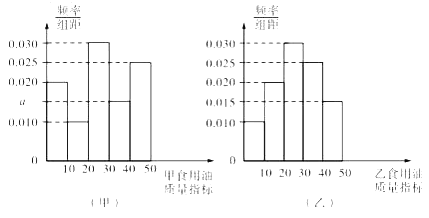
(Ⅰ)写出频率分布直方图(甲)中![]() 的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为
的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为![]() ,
,![]() ,试比较
,试比较![]() ,
,![]() 的大小(只要求写出答案);
的大小(只要求写出答案);
(Ⅱ)估计在甲、乙两种食用油中随机抽取1捅,恰有一桶的质量指标大于20;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,设
,设![]() 表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的桶数,求
表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的桶数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区问的中点值作代表,计算得![]()
②若![]()
![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(Ⅰ)求所取3张卡片上的数字完全相同的概率;
(Ⅱ)![]() 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求![]() 的分布列与数学期望.
的分布列与数学期望.
(注:若三个数![]() 满足
满足![]() ,则称
,则称![]() 为这三个数的中位数).
为这三个数的中位数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年7月24日,长春长生生物科技有限责任公司先被查出狂犬病疫苗生产记录造假,因此,疫苗在上市前必须经过严格的检测,以保证疫苗使用的安全和有效.某生物制品研究所将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如表:现从所有试验小白鼠中任取一只,取到“注射疫苗”小白鼠的概率为![]() .
.
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 20 | x | A |
注射疫苗 | 30 | y | B |
总计 | 50 | 50 | 100 |
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
(1)求2×2列联表中的数据![]() 的值;
的值;
(2)能否有99.9%把握认为注射此种疫苗有效?
附:![]() ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点(如图1).将
中点(如图1).将![]() 沿
沿![]() 折起到图2中
折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.
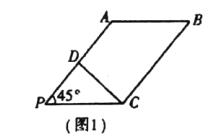
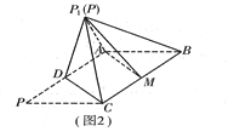
(1)将![]() 沿
沿![]() 折起的过程中,
折起的过程中, ![]() 平面
平面![]() 是否成立?并证明你的结论;
是否成立?并证明你的结论;
(2)若![]() ,过
,过![]() 的平面交
的平面交![]() 于点
于点![]() ,且
,且![]() 为
为![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
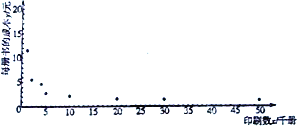
|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为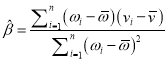 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于正整数集合![]() (
(![]() ,
,![]() ),如果去掉其中任意一个元素
),如果去掉其中任意一个元素![]() (
(![]() )之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
)之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合![]() 为“和谐集”.
为“和谐集”.
(1)判断集合![]() 是否为“和谐集”,并说明理由;
是否为“和谐集”,并说明理由;
(2)求证:集合![]() 是“和谐集”;
是“和谐集”;
(3)求证:若集合![]() 是“和谐集”,则集合
是“和谐集”,则集合![]() 中元素个数为奇数.
中元素个数为奇数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com