
【题目】已知函数f(x)=|x+1|+2|x﹣m|
(1)当m=2时,求f(x)≤9的解集;
(2)若f(x)≤2的解集不是空集,求实数m的取值范围.
【答案】(1)[﹣2,4](2)[﹣3,1]
【解析】
(1)当m=2时,函数f(x)=|x+1|+2|x﹣2|≤9,对x分类讨论,分别在三个区间![]() ,去掉绝对值求解不等式即可求得解集;
,去掉绝对值求解不等式即可求得解集;
(2)若f(x)≤2的解集不是空集,转化为f(x)min≤2成立,又根据|x+1|+|x﹣m|≥|m+1|恒成立,f(x)min=|m+1|≤2,解得﹣3≤m≤1.
(1)当m=2时,f(x)=|x+1|+2|x﹣2|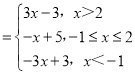 .
.
∵f(x)≤9,∴![]() 或
或![]() 或
或![]() ,
,
∴2<x≤4或﹣1≤x≤2或﹣2≤x<﹣1,
∴﹣2≤x≤4,
∴不等式的解集为[﹣2,4];
(2)∵f(x)≤2的解集不是空集,
∴f(x)min≤2.
∵|x+1|+|x﹣m|≥|m+1|,|x﹣m|≥0,
∴f(x)=|x+1|+2|x﹣m|≥|m+1|,当且仅当x=m时取等号,
∴|m+1|≤2,∴﹣3≤m≤1,
∴实数m的取值范围为[﹣3,1].


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:高中数学 来源: 题型:
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛,经过初赛、复赛,甲、乙两个代表队(每队![]() 人)进入了决赛,规定每人回答一个问题,答对为本队赢得
人)进入了决赛,规定每人回答一个问题,答对为本队赢得![]() 分,答错得
分,答错得![]() 分,假设甲队中每人答对的概率均为
分,假设甲队中每人答对的概率均为![]() ,乙队中
,乙队中![]() 人答对的概率分別为
人答对的概率分別为![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(1)求![]() 的分布列;
的分布列;
(2)求甲、乙两队总得分之和等于![]() 分且甲队获胜的概率.
分且甲队获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,函数
,函数![]() ,记
,记![]() .把函数
.把函数![]() 的最大值
的最大值![]() 称为函数
称为函数![]() 的“线性拟合度”.
的“线性拟合度”.
(1)设函数![]() ,
,![]() ,
,![]() ,求此时函数
,求此时函数![]() 的“线性拟合度”
的“线性拟合度”![]() ;
;
(2)若函数![]() ,
,![]() 的值域为
的值域为![]() (
(![]() ),
),![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,
,![]() ,求
,求![]() 的值,使得函数
的值,使得函数![]() 的“线性拟合度”
的“线性拟合度”![]() 最小,并求出
最小,并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,SA⊥底面ABCD,底面ABCD是平行四边形,E是线段SD上一点.

(1)若E是SD的中点,求证:SB∥平面ACE;
(2)若SA=AB=AD=2,SC=2![]() ,且DE
,且DE![]() DS,求二面角S﹣AC﹣E的余弦值.
DS,求二面角S﹣AC﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 其中a为常数,设e为自然对数的底数.
其中a为常数,设e为自然对数的底数.
(1)当![]() 时,求
时,求![]() 过切点为
过切点为![]() 的切线方程;
的切线方程;
(2)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求a的值;
,求a的值;
(3)若不等式![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() 过点(0,1)且离心率
过点(0,1)且离心率![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设动直线l与两定直线l1:x﹣y=0和l2:x+y=0分别交于P,Q两点.若直线l总与椭圆E有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 分别是棱长为2的正方体
分别是棱长为2的正方体![]() 的棱
的棱![]() 的中点.如图,以
的中点.如图,以![]() 为坐标原点,射线
为坐标原点,射线![]() 、
、![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正半轴,建立空间直角坐标系.
轴的正半轴,建立空间直角坐标系.

(1)求向量![]() 与
与![]() 的数量积;
的数量积;
(2)若点![]() 分别是线段
分别是线段![]() 与线段
与线段![]() 上的点,问是否存在直线
上的点,问是否存在直线![]() ,
,![]() 平面
平面![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com