
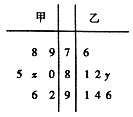
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是89.
(1)求![]() 和
和![]() 的值;
的值;
(2)计算乙班7位学生成绩的方差![]() .
.
(3)从成绩在90分以上的学生中随机抽取两名学生,求乙班至少有一名学生的概率.
【答案】(1)x=5,y=3;(2)40;(3)![]()
【解析】试题分析:(1)根据平均数计算公式可求![]() ,中位数是指将一组数据按照从小到大或者从大到小的顺序排成一列,如果是奇数个数,中位数是最中间的数;如果是偶数个数,中位数是最中间两个数的平均数,由题知
,中位数是指将一组数据按照从小到大或者从大到小的顺序排成一列,如果是奇数个数,中位数是最中间的数;如果是偶数个数,中位数是最中间两个数的平均数,由题知![]() ;(2)甲班七名学生成绩已知,代入方差计算公式即可;(3)记事件
;(2)甲班七名学生成绩已知,代入方差计算公式即可;(3)记事件![]() =“从中抽取两名学生,甲班至少有一名学生”,把成绩在90分以上的学生编号,列出从中抽取两名学生的基本事件总数以及事件
=“从中抽取两名学生,甲班至少有一名学生”,把成绩在90分以上的学生编号,列出从中抽取两名学生的基本事件总数以及事件![]() 包含的基本事件总数,代入古典概型的概率计算公式可求;至少、至多问题的概率还可以根据对立事件的概率来求,即
包含的基本事件总数,代入古典概型的概率计算公式可求;至少、至多问题的概率还可以根据对立事件的概率来求,即![]() .
.
试题解析:(1)由![]() =85,得
=85,得![]() ,所以
,所以![]() =5,将数字按照从小到大的顺序排列,第四个数字是中位数,所以
=5,将数字按照从小到大的顺序排列,第四个数字是中位数,所以![]() ;
;
(2)![]() =40;
=40;
(3)成绩在90分以上的学生共有5名,其中甲班有两名,记为a,b,乙班3名,记为1,2,3,从中任取两名,基本事件为有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共10个,记事件
,共10个,记事件![]() =“从中抽取两名学生,甲班至少有一名学生”,则事件
=“从中抽取两名学生,甲班至少有一名学生”,则事件![]() 包含的基本事件有
包含的基本事件有![]() ,
, ![]() ,
, ![]() ,共7个,所以
,共7个,所以![]() .
.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】设函数![]()
(1)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)若![]() 在
在![]() 内有两个极值点,求负数
内有两个极值点,求负数![]() 的取值范围;
的取值范围;
(3)已知 ,若对任意实数
,若对任意实数![]() ,总存在实数
,总存在实数![]() ,使得
,使得![]() 成立,求正实数
成立,求正实数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且Sn=2n﹣1.数列{bn}满足b1=2,bn+1﹣2bn=8an .
(1)求数列{an}的通项公式.
(2)证明:数列{ ![]() }为等差数列,并求{bn}的通项公式.
}为等差数列,并求{bn}的通项公式.
(3)求{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家父母记录了女儿玥玥的年龄(岁)和身高(单位cm)的数据如下:
年龄x | 6 | 7 | 8 | 9 |
身高y | 118 | 126 | 136 | 144 |
(1)试求y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]()
(2)试预测玥玥10岁时的身高.(其中, ![]() =
= 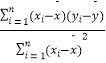 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数{an}:a1=t,n2Sn+1=n2(Sn+an)+an2 , n=1,2,….
(1)设{an}为等差数列,且前两项和S2=3,求t的值;
(2)若t= ![]() ,证明:
,证明: ![]() ≤an<1.
≤an<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是棱
分别是棱![]() ,
, ![]() ,
, ![]() ,
, ![]() 的中点,点
的中点,点![]() ,
, ![]() 分别在棱
分别在棱![]() ,
, ![]() 上移动,且
上移动,且![]() .
.
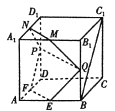
(1)当![]() 时,证明:直线
时,证明:直线![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使面
,使面![]() 与面
与面![]() 所成的二面角为直二面角?若存在,求出
所成的二面角为直二面角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (k>0).
(k>0).
(1)若f(x)>m的解集为{x|x<﹣3或x>﹣2},求不等式5mx2+ ![]() x+3>0的解集;
x+3>0的解集;
(2)若存在x>3使得f(x)>1成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了普及环保知识,增强环保意识,某校从理科甲班抽取60人,从文科乙班抽取50人参加环保知识测试.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
(Ⅰ)根据题目完成![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为环保知识成绩优秀与学生的文理分类有关.
的把握认为环保知识成绩优秀与学生的文理分类有关.
(Ⅱ)现已知![]() ,
, ![]() ,
, ![]() 三人获得优秀的概率分别为
三人获得优秀的概率分别为![]() ,
, ![]() ,
, ![]() ,设随机变量
,设随机变量![]() 表示
表示![]() ,
, ![]() ,
, ![]() 三人中获得优秀的人数,求
三人中获得优秀的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
附:  ,
, ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 若4Sn=(2n﹣1)an+1+1,且a1=1.
(1)求数列{an}的通项公式;
(2)设cn= ![]() ,数列{cn}的前n项和为Tn .
,数列{cn}的前n项和为Tn .
①求Tn;
②对于任意的n∈N*及x∈R,不等式kx2﹣6kx+k+7+3Tn>0恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com