
【题目】高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,B、E、F为山脚两侧共线的三点,在山顶A处测得这三点的俯角分别为![]() 、
、![]() 、
、![]() ,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
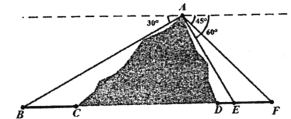
(1)求出线段AE的长度;
(2)求出隧道CD的长度.
科目:高中数学 来源: 题型:
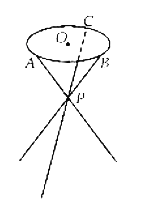
【题目】如图,小凳凳面为圆形,凳脚为三根细钢管.考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点![]() 与凳面圆形的圆心
与凳面圆形的圆心![]() 的连线垂直于凳面和地面,且
的连线垂直于凳面和地面,且![]() 分细钢管上下两段的比值为
分细钢管上下两段的比值为![]() ,三只凳脚与地面所成的角均为
,三只凳脚与地面所成的角均为![]() .若
.若![]() 、
、![]() 、
、![]() 是凳面圆周的三等分点,
是凳面圆周的三等分点,![]() 厘米,求凳子的高度
厘米,求凳子的高度![]() 及三根细钢管的总长度(精确到
及三根细钢管的总长度(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形ABCD为矩形,AB=2AD=4,M为AB的中点,将△ADM沿DM折起,得到四棱锥A1﹣DMBC,设A1C的中点为N,在翻折过程中,得到如下有三个命题:①BN∥平面A1DM;②三棱锥N﹣DMC的最大体积为![]() ;③在翻折过程中,存在某个位置,使得DM⊥A1C.其中正确命题的序号为_____.
;③在翻折过程中,存在某个位置,使得DM⊥A1C.其中正确命题的序号为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为
)的焦距为![]() ,且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于
,且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于![]() 、
、![]() ,且在椭圆C上存在点M,使得:
,且在椭圆C上存在点M,使得:![]() (其中O为坐标原点),则称直线l具有性质H.
(其中O为坐标原点),则称直线l具有性质H.
(1)求椭圆C的方程;
(2)若直线l垂直于x轴,且具有性质H,求直线l的方程;
(3)求证:在椭圆C上不存在三个不同的点P、Q、R,使得直线![]() 、
、![]() 、
、![]() 都具有性质H.
都具有性质H.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业参加![]() 项目生产的工人为
项目生产的工人为![]() 人,平均每人每年创造利润
人,平均每人每年创造利润![]() 万元.根据现实的需要,从
万元.根据现实的需要,从![]() 项目中调出
项目中调出![]() 人参与
人参与![]() 项目的售后服务工作,每人每年可以创造利润
项目的售后服务工作,每人每年可以创造利润![]() 万元(
万元(![]() ),
),![]() 项目余下的工人每人每年创造利图需要提高
项目余下的工人每人每年创造利图需要提高![]()
(1)若要保证![]() 项目余下的工人创造的年总利润不低于原来
项目余下的工人创造的年总利润不低于原来![]() 名工人创造的年总利润,则最多调出多少人参加
名工人创造的年总利润,则最多调出多少人参加![]() 项目从事售后服务工作?
项目从事售后服务工作?
(2)在(1)的条件下,当从![]() 项目调出的人数不能超过总人数的
项目调出的人数不能超过总人数的![]() 时,才能使得
时,才能使得![]() 项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数
项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福彩是利国利民游戏,其刮刮乐之《蓝色奇迹》:如图(1)示例,刮开票面看到最左侧一列四个两位数字为“我的号码”,最上行四个两位数为“中奖号码”,这八个两位数是00至99这一百个数字随机产生的,若两个数字相同即中得其相交线上的奖金,奖金可以累加.小明买的一张《蓝色奇迹》刮刮乐如图(2),除了一个“我的号码”外,他已经刮开票面上其它所有数字,依据目前的信息,小明从这张刮刮乐得到的奖金额高于600元的概率为(无所得税)( )


图(1) 图(2)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() 的方程为
的方程为![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系![]() .
.
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与曲线
,与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() ,抛物线
,抛物线![]() 的焦点F是椭圆
的焦点F是椭圆![]() 的顶点.
的顶点.
(1)求![]() 与
与![]() 的标准方程;
的标准方程;
(2)![]() 上不同于F的两点P,Q满足以PQ为直径的圆经过F,且直线PQ与
上不同于F的两点P,Q满足以PQ为直径的圆经过F,且直线PQ与![]() 相切,求
相切,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部![]() 名同学参加学校社团的情况,数据如下表:(单位:人)
名同学参加学校社团的情况,数据如下表:(单位:人)
参加书法社 | 未参加书法社 | |
参加辩论社 |
|
|
未参加辩论社 |
|
|
(1)从该班随机选![]() 名同学,求该同学至少参加一个社团的概率;
名同学,求该同学至少参加一个社团的概率;
(2)在既参加书法社又参加辩论社的![]() 名同学中,有
名同学中,有![]() 名男同学
名男同学![]() ,
,![]() 名女同学
名女同学![]() .现从这
.现从这![]() 名同学中男女姓各随机选
名同学中男女姓各随机选![]() 人(每人被选到的可能性相同).
人(每人被选到的可能性相同).
(i)列举出所有可能结果;
(ii)设![]() 为事件“
为事件“![]() 被选中且
被选中且![]() 未被选中”,求事件
未被选中”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com