
【题目】设函数f(x)=|3﹣2x|+|2x﹣a|
(1)当a=1时,求不等式f(x)≤3的解集;
(2)若存在x∈R使得不等式f(x)≤t+![]() +2对任意t>0恒成立,求实数a的取值范围.
+2对任意t>0恒成立,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)解法一:利用分类讨论法去掉绝对值,解对应的不等式即可;
解法二:利用分段函数表示f(x),作出y=f(x)和直线y=3的图象,利用图象求出不等式的解集;
(2)由题意可得f(x)的最小值不大于t![]() 2的最小值,利用绝对值不等式求出f(x)的最小值,利用基本不等式求出t
2的最小值,利用绝对值不等式求出f(x)的最小值,利用基本不等式求出t![]() 2的最小值,
2的最小值,
再列不等式求得实数a的取值范围.
(1)解法一:当a=1时,f(x)=|3﹣2x|+|2x﹣1|;
当x![]() 时,不等式f(x)≤3可化为:﹣2x+1﹣2x+3≤3,
时,不等式f(x)≤3可化为:﹣2x+1﹣2x+3≤3,
解得x![]() ,此时
,此时![]() x
x![]() ;
;
当![]() x
x![]() 时,不等式f(x)≤3可化为为:2x﹣1﹣2x+3≤3,
时,不等式f(x)≤3可化为为:2x﹣1﹣2x+3≤3,
此不等式恒成立,此时得![]() x
x![]() ;
;
当x![]() 时,不等式f(x)≤3可化为:2x﹣1+2x﹣3≤3,
时,不等式f(x)≤3可化为:2x﹣1+2x﹣3≤3,
解得得x![]() ,此时
,此时![]() x
x![]() ,
,
综上知,![]() x
x![]() ,即不等式的解集为[
,即不等式的解集为[![]() ,
,![]() ];
];
解法二:利用分段函数表示f(x)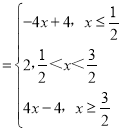 ;
;
作出y=f(x)和直线y=3的图象,如图所示:
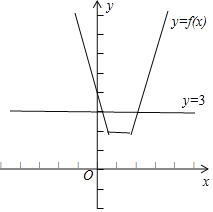
由f(x)=3解得:x![]() 或x
或x![]() ,
,
由图象可得不等式的解集为[![]() ,
,![]() ];
];
(2)由f(x)=|3﹣2x|+|2x﹣a|≥|3﹣2x+2x﹣a|=|3﹣a|=|a﹣3|,
即f(x)的最小值为|a﹣3|,
由t![]() 2≥2
2≥2![]() 2=6,当且仅当t
2=6,当且仅当t![]() ,即t=2时,取等号,
,即t=2时,取等号,
因为存在x∈R,使得不等式f(x)≤t![]() 2对任意t>0恒成立,
2对任意t>0恒成立,
所以|a﹣3|≤6,解得﹣3≤a≤9;
所以实数a的取值范围是﹣3≤a≤9.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】给出下列命题:
①过圆心和圆上的两点有且只有一个平面
②若直线![]() 与平面
与平面![]() 平行,则
平行,则![]() 与平面
与平面![]() 内的任意一条直线都没有公共点
内的任意一条直线都没有公共点
③若直线![]() 上有无数个点不在平面
上有无数个点不在平面![]() 内,则
内,则![]()
④如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行
⑤垂直于同一个平面的两条直线平行
其中正确的命题的个数是![]()
![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①一个命题的否命题为真,则它的逆命题一定为真;
②若p![]() q为假命题,则p,q均为假命题;
q为假命题,则p,q均为假命题;
③命题“若x2 -3x+2=0,则x=2”的否命题为“若x2 -3x+2=0,则x≠2”;
④“若a2+b2=0,则a, b全为0”的逆否命题是“若a, b全不为0,则a2+b2≠0”其中正确的命题序号是( )
A.①B.①③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,
,![]() ,
,![]() 是
是![]() 的动点,过点
的动点,过点![]() 作
作![]() 的垂线,线段
的垂线,线段![]() 的中垂线交
的中垂线交![]() 于点
于点![]() ,
,![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)过![]() 且与坐标轴不垂直的直线交曲线
且与坐标轴不垂直的直线交曲线![]() 于
于![]() 两点,若以线段
两点,若以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 相切,求直线
相切,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了推广一种新饮料,某饮料生产企业开展了有奖促销活动:将6罐这种饮料装一箱,每箱中都放置2罐能够中奖的饮料.若从一箱中随机抽出2罐,能中奖的概率为多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对心肺疾病入院的![]() 人进行问卷调查,得到了如下的列联表:
人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
(1)用分层抽样的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)在上述抽取的![]() 人中选
人中选![]() 人,求恰好有
人,求恰好有![]() 名女性的概率;
名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,你有多大把握认为心肺疾病与性别有关?
,你有多大把握认为心肺疾病与性别有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:  ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
如图,四边形ABCD为梯形,AB//CD,![]() 平面ABCD,
平面ABCD,![]()
![]() 为BC的中点.
为BC的中点.
(1)求证:平面![]() 平面PDE.
平面PDE.
 (2)在线段PC上是否存在一点F,使得PA//平面BDF?若存在,指出点F的位置,并证明;若不存在,请说明理由.
(2)在线段PC上是否存在一点F,使得PA//平面BDF?若存在,指出点F的位置,并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sinxcosx+cos2x-
sinxcosx+cos2x-![]() .
.
(Ⅰ)求函数f(x)的最小正周期及单调递增区间;
(Ⅱ)将函数f(x)图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数g(x)的图象.若关于x的方程g(x)-k=0,在区间[0,![]() ]上有实数解,求实数k的取值范围.
]上有实数解,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com