
【题目】△ABC中内角A,B,C的对边分别为a,b,c,向量 ![]() =(2sinB,﹣
=(2sinB,﹣ ![]() ),
), ![]() =(cos2B,2cos2
=(cos2B,2cos2 ![]() ﹣1)且
﹣1)且 ![]() ∥
∥ ![]() .
.
(1)求锐角B的大小;
(2)如果b=2,求△ABC的面积S△ABC的最大值.
【答案】
(1)解:∵ ![]() =(2sinB,﹣
=(2sinB,﹣ ![]() ),
), ![]() =(cos2B,2cos2
=(cos2B,2cos2 ![]() ﹣1)且
﹣1)且 ![]() ∥
∥ ![]() ,
,
∴2sinB(2cos2 ![]() ﹣1)=﹣
﹣1)=﹣ ![]() cos2B,
cos2B,
∴2sinBcosB=﹣ ![]() cos2B,即sin2B=﹣
cos2B,即sin2B=﹣ ![]() cos2B,
cos2B,
∴tan2B=﹣ ![]() ,
,
又B为锐角,∴2B∈(0,π),
∴2B= ![]() ,
,
则B= ![]() ;
;
(2)解:当B= ![]() ,b=2,
,b=2,
由余弦定理cosB= ![]() 得:a2+c2﹣ac﹣4=0,
得:a2+c2﹣ac﹣4=0,
当B= ![]() ,b=2,
,b=2,
由余弦定理cosB= ![]() 得:a2+c2+ac﹣4=0,
得:a2+c2+ac﹣4=0,
又a2+c2≥2ac,代入上式得:ac≤4(当且仅当a=c=2时等号成立),
∴S△ABC= ![]() acsinB=
acsinB= ![]() ac≤
ac≤ ![]() (当且仅当a=c=2时等号成立),
(当且仅当a=c=2时等号成立),
则S△ABC的最大值为 ![]()
【解析】(1)由两向量的坐标及两向量平行,利用平面向量平行时满足的条件列出关系式,利用二倍角的正弦、余弦函数公式及同角三角函数间的基本关系化简,求出tan2B的值,由B为锐角,得到2B的范围,利用特殊角的三角函数值即可求出B的度数;(2)由B的度数求出sinB及cosB的值,进而由b及cosB的值,利用余弦定理列出关系式,再利用基本不等式化简求出ac的最大值,再由ac的最大值及sinB的值,利用三角形的面积公式即可求出三角形ABC面积的最大值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的方程x2﹣ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,若“p或q”是真命题,“p且q”是假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=﹣13,a6+a8=﹣2,且an﹣1=2an﹣an+1(n≥2),则数列{ ![]() }的前13项和为( )
}的前13项和为( )
A.![]()
B.﹣ ![]()
C.![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为等比数列{an}的前n项和且S4=S3+3a3 , a2=9.
(1)求数列{an}的通项公式
(2)设bn=(2n﹣1)an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象经过下列哪种变换可以得到函数y=cos2x的图象( )
A.先向左平移 ![]() 个单位,然后再沿x轴将横坐标压缩到原来的
个单位,然后再沿x轴将横坐标压缩到原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
B.先向左平移 ![]() 个单位,然后再沿x轴将横坐标伸长到原来的2倍(纵坐标不变)
个单位,然后再沿x轴将横坐标伸长到原来的2倍(纵坐标不变)
C.先向左平移 ![]() 个单位,然后再沿x轴将横坐标压缩到原来的
个单位,然后再沿x轴将横坐标压缩到原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
D.先向左平移 ![]() 个单位,然后再沿x轴将横坐标伸长到原来的2倍(纵坐标不变)
个单位,然后再沿x轴将横坐标伸长到原来的2倍(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆M:x2+y2﹣2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1 , l2 , 切点为B,C. 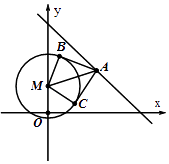
(1)当a=0时,求直线l1 , l2的方程;
(2)是否存在点A,使得 ![]() =﹣2?若存在,求出点A的坐标,若不存在,请说明理由.
=﹣2?若存在,求出点A的坐标,若不存在,请说明理由.
(3)求证当点A在直线l运动时,直线BC过定点P0 .
(附加题)问:第(3)问的逆命题是否成立?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)是奇函数,且在(0,+∞)上是增函数,又f(﹣3)=0,则(x﹣1)f(x)<0的解是( )
A.(﹣3,0)∪(1,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(3,+∞)
D.(﹣3,0)∪(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间. 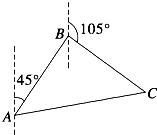
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com