
分析 ①,定点(2,1)在定直线3x+4y-10=0上,到定点(2,1)的距离与到定直线3x+4y-10=0的距离相等的点的轨迹不是抛物线.
②,利用双曲线的定义,即可得出结论.
③,求出方程的两根即可得到答案.
④,设P(x,y),由$\overrightarrow{OP}$=($\overrightarrow{OA}$+$\overrightarrow{OB}$),得B(x-m,y-n),把B的坐标代入圆x2+y2=1得到P的轨迹仍为圆,
解答 解:对于①,因为点(-1,2)在直线2x+3y-4=0上,∴到点(-1,2)和到直线2x+3y-4=0距离相等的点的轨迹是过定点与此直线垂直的直线,不是抛物线,故①错;
对于②,中当0<k<|AB|时是双曲线的一支,当k=|AB|时,表示射线,∴②错;
对于③,方程4x2-8x+3=0的两根为$\frac{1}{2}$、$\frac{3}{2}$可以分别作为椭圆和双曲线的离心率,故③正确;
对于④,设单位圆O的方程为x2+y2=1,点A(m,n),P(x,y),由$\overrightarrow{OP}$=($\overrightarrow{OA}$+$\overrightarrow{OB}$),得B(x-m,y-n),因为B在已知圆上,把B的坐标代入圆x2+y2=1得到P的轨迹仍为圆,故错;
故答案为:③.
点评 本题考查了有关圆锥曲线的命题真假的判定,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{11}{27}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
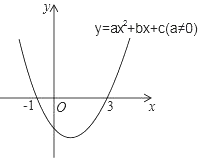 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0;②当-1≤x≤3时,y<0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0;②当-1≤x≤3时,y<0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0其中正确的是( )| A. | ①②④ | B. | ①④ | C. | ①②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5-2a | B. | 2a-5 | C. | 1 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com