
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若![]() 时,不等式
时,不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的单调递增区间为
的单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() .(2)
.(2)![]()
【解析】
试题分析:(1)当![]() 求导,可得
求导,可得![]() 的单调区间;(2)首先,要保证
的单调区间;(2)首先,要保证![]() 由意义,可得
由意义,可得![]() ;由题意得,不等式
;由题意得,不等式![]() 对于任意的
对于任意的![]() 恒成立,构造新函数
恒成立,构造新函数![]() ,
,![]() ,求导研究函数
,求导研究函数![]() 的性质,分情况讨论当
的性质,分情况讨论当![]() 时,不满足题意;当
时,不满足题意;当![]() 时,要使
时,要使![]() 时,不等式
时,不等式![]() 成立,需
成立,需![]() ,即
,即![]() ,此时要证
,此时要证![]() ,继续构造函数
,继续构造函数![]() ,求导可证得
,求导可证得![]() 在
在![]() 上单调递增,
上单调递增,![]() . 即
. 即![]() ,问题解决.
,问题解决.
试题解析:(1)当![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,,
时,,![]() 单调递减.
单调递减.
综上,![]() 的单调递增区间为
的单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() .
.
(2) 由题意得,![]() 时,
时,![]() 恒成立,可得
恒成立,可得![]() .……①
.……①
由题意得,不等式![]() 对于任意的
对于任意的![]() 恒成立.
恒成立.
设![]() ,
,![]() .
.![]() .
.
当![]() 时,
时,![]() ,不满足题意;
,不满足题意;
当![]() 时,要使
时,要使![]() 时,不等式
时,不等式![]() 成立,
成立,
须![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,
,
设![]() ,
,![]() .
.
显然在![]() 上单调递增,所以
上单调递增,所以![]() .
.
所以![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
即![]() . ……②
. ……②
由①②可知![]() 时,满足题意.
时,满足题意.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如表所示:
(天)之间的关系如表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)请根据表中数据在所给网格中绘制散点图;
(Ⅱ)请根据表中提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留2位有效数字);
保留2位有效数字);
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店买进土豆40吨,则预计可以销售多少天(计算结果保留整数)?
附: 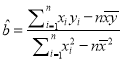 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“足寒伤心,民寒伤国”,精准扶贫是巩固温饱成果、加快脱贫致富、实现中华民族伟大“中国梦”的重要保障.某地政府在对石山区乡镇企业实施精准扶贫的工作中,准备投入资金将当地农产品进行二次加工后进行推广促销,预计该批产品销售量![]() 万件(生产量与销售量相等)与推广促销费
万件(生产量与销售量相等)与推广促销费![]() 万元之间的函数关系为
万元之间的函数关系为![]() (其中推广促销费不能超过3万元).已知加工此批农产品还要投入成本
(其中推广促销费不能超过3万元).已知加工此批农产品还要投入成本![]() 万元(不包含推广促销费用),若加工后的每件成品的销售价格定为
万元(不包含推广促销费用),若加工后的每件成品的销售价格定为![]() 元/件.
元/件.
(1)试将该批产品的利润![]() 万元表示为推广促销费
万元表示为推广促销费![]() 万元的函数;(利润
万元的函数;(利润![]() 销售额
销售额![]() 成本
成本![]() 推广促销费)
推广促销费)
(2)当推广促销费投入多少万元时,此批产品的利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 从
从![]() ,
, ![]() ,
, ![]() ,
, ![]() 四个数中任取的一个数,
四个数中任取的一个数, ![]() 是从
是从![]() ,
, ![]() ,
, ![]() 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过![]()
![]() 关者奖励
关者奖励![]() 件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.

(Ⅰ)估计小明在1次游戏中所得奖品数的期望值;
(Ⅱ)估计小明在3 次游戏中至少过两关的平均次数;
(Ⅲ)估计小明在3 次游戏中所得奖品超过30件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生每次投篮的命中概率都为![]() .现采用随机模拟的方法求事件的概率:先由计算器产生0到9之间的整数值随机数,制定1、2、3、4表示命中,5、6、7、8、9、0表示不命中;再以每3个随机数为一组,代表三次投篮的结果.经随机模拟产生如下20组随机数:989 537 113 730 488 556 027 393 257 431 683 569 458 812 932 271 925 191 966 907,据此统计,该学生三次投篮中恰有一次命中的概率约为__________.
.现采用随机模拟的方法求事件的概率:先由计算器产生0到9之间的整数值随机数,制定1、2、3、4表示命中,5、6、7、8、9、0表示不命中;再以每3个随机数为一组,代表三次投篮的结果.经随机模拟产生如下20组随机数:989 537 113 730 488 556 027 393 257 431 683 569 458 812 932 271 925 191 966 907,据此统计,该学生三次投篮中恰有一次命中的概率约为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定下列函数:①f(x)= ![]() ②f(x)=﹣|x|③f(x)=﹣2x﹣1 ④f(x)=(x﹣1)2 , 满足“对任意x1 , x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的条件是( )
②f(x)=﹣|x|③f(x)=﹣2x﹣1 ④f(x)=(x﹣1)2 , 满足“对任意x1 , x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的条件是( )
A.①②③
B.②③④
C.①②④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1﹣ ![]() (a>0且a≠1)是定义在R上的奇函数.
(a>0且a≠1)是定义在R上的奇函数.
(1)求a的值;
(2)求f(x)的值域;
(3)若关于x的方程|f(x)(2x+1)|=m有1个实根,求实数m的取值范围;
(4)当x∈(0,1]时,tf(x)≥2x﹣2恒成立,求实数t取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com