练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下面程序的功能是(　　)

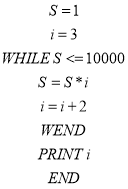
    A. 求1×2×3×4×…×10 00的值

    B. 求2×4×6×8×…×10 000的值

    C. 求3×5×7×9×…×10 001的值

    D. 求满足1×3×5×…×n＞10 000的最小正整数n

    【答案】D

    【解析】S是累乘变量，i是计数变量，每循环一次，S乘以i一次且i增加2.

    当S＞10 000时停止循环，输出的i值是使1×3×5×…×n＞10 000成立的最小正整数n.选D.

    点睛: 循环结构程序框图的注意事项

    第一，要明确是当型循环结构还是直到型循环结构，根据各自特点执行循环体；第二，要明确框图中的累加变量，明确每一次执行循环体前和执行循环体后，变量的值发生的变化；第三，要明确循环终止的条件是什么，什么时候要终止执行循环体．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在投掷骰子试验中，根据向上的点数可以定义许多事件，如：A={出现1点}，B={出现3点或4点}，C={出现的点数是奇数}，D={出现的点数是偶数}.

    (1)说明以上4个事件的关系.

    (2)求两两运算的结果.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线的参数方程为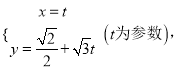若以直角坐标系xOy的O点为极点，Ox方向为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程为

    (1)求直线的斜率和曲线C的直角坐标方程；

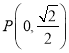    (2)若直线与曲线C交于A、B 两点，设点，求|PA|+|PB|.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司有五辆汽车，其中两辆汽车的车牌尾号均为1. 两辆汽车的车牌尾号均为2， 车的车牌尾号为6，已知在非限行日，每辆车可能出车或不出车， 三辆汽车每天出车的概率均为， 两辆汽车每天出车的概率均为，且五辆汽车是否出车相互独立，该公司所在地区汽车限行规定如下：

    车牌尾号

    0和5

    1和6

    2和7

    3和8

    4和9

    限行日

    星期一

    星期二

    星期三

    星期四

    星期五

    （1）求该公司在星期一至少有2辆汽车出国的概率；

    （2）设表示该公司在星期二和星期三两天出车的车辆数之和，求的分布列及期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在哈尔滨的中央大街的步行街同侧有6块广告牌，牌的底色可选用红、蓝两种颜色，若要求相邻两块牌的底色不都为蓝色，则不同的配色方案共有（ ）

    A. 20 B. 21 C. 22 D. 24

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是抛物线的焦点， 为抛物线上不同的两点， 分别是抛物线在点、点处的切线， 是的交点．

    （1）当直线经过焦点时，求证：点在定直线上；

    （2）若，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完5局仍未出现连胜，则判定获胜局数多者赢得比赛．假设每局甲获胜的概率为，乙获胜的概率为，各局比赛结果相互独立．

    (1)求甲在4局以内(含4局)赢得比赛的概率；

    (2)记X为比赛决出胜负时的总局数，求X的分布列和均值(数学期望)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 在区间内单调递减，在区间内单调递增，且在上有三个零点，1是其中一个零点.

    （1）求的取值范围；

    （2）若直线在曲线的上方部分所对应的的集合为，试求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥的底面是菱形， 平面， ，点为的中点.

    （1）求证： 平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案