
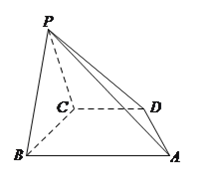
【题目】如图,在等腰梯形![]() 中,
中, ![]() ,上底
,上底![]() ,下底
,下底![]() ,点
,点![]() 为下底
为下底![]() 的中点,现将该梯形中的三角形
的中点,现将该梯形中的三角形![]() 沿线段
沿线段![]() 折起,形成四棱锥
折起,形成四棱锥![]() .
.

(1)在四棱锥![]() 中,求证:
中,求证: ![]() ;
;
(2)若平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】试题分析:(1)由![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,得三角形
的中点,得三角形![]() 沿线段
沿线段![]() 折起后可得四边形
折起后可得四边形![]() 为菱形,边长为
为菱形,边长为![]() ,
, ![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,可证
,可证![]() ,
, ![]() ,即可证
,即可证![]() 平面
平面![]() ,从而
,从而![]() 平面
平面![]() ,即可得证;(2)以
,即可得证;(2)以![]() 为坐标原点,建立空间直角坐标系,由(1)可证
为坐标原点,建立空间直角坐标系,由(1)可证![]() 为平面
为平面![]() 与平面
与平面![]() 所成二面角的平面角,从而求出
所成二面角的平面角,从而求出![]() ,
, ![]() ,
, ![]() ,
, ![]() ,再求出平面
,再求出平面![]() 的一个法向量,即可求出直线
的一个法向量,即可求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
试题解析:(1)证明:由三角形![]() 沿线段
沿线段![]() 折起前,
折起前, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,得三角形
的中点,得三角形![]() 沿线段
沿线段![]() 折起后,四边形
折起后,四边形![]() 为菱形,边长为
为菱形,边长为![]() ,
, ![]() ,如图,
,如图,
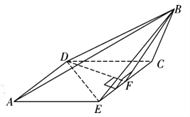
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,
,
∵由题得![]() 和
和![]() 均为正三角形,
均为正三角形,
∴![]() ,
, ![]() ,
,
又![]()
∴![]() 平面
平面![]() ,
,
∵![]() ∥
∥![]()
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(2)解:以![]() 为坐标原点,建立如图的空间直角坐标系,
为坐标原点,建立如图的空间直角坐标系,
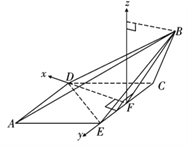
由![]() 平面
平面![]() ,有
,有![]() 轴在平面
轴在平面![]() 内,
内,
在(1)中,∵![]() ,
, ![]() ,
,
∴![]() 为平面
为平面![]() 与平面
与平面![]() 所成二面角的平面角,
所成二面角的平面角,
∴![]() ,
,
而![]() ,∴
,∴![]() 且
且![]() ,
,
得点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的竖坐标为
的竖坐标为![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, 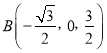 ,
,
故![]() ,
, 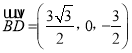 ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴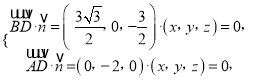 得
得
令![]() ,得
,得![]() ,
, ![]() ,∴平面
,∴平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴![]()
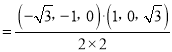
![]() ,
,
∵直线![]() 与平面
与平面![]() 所成角为锐角或直角,
所成角为锐角或直角,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了治理大气污染,某市2017年初采用了一系列措施,比如“煤改电”,“煤改气”,“国Ⅰ,Ⅱ轻型汽油车限行”,“整治散乱污染企业”等.下表是该市2016年和2017年12月份的空气质量指数(AQI)(AQI指数越小,空气质量越好)统计表.
表1:2016年12月AQI指数表:单位(![]() )
)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
AQI | 47 | 123 | 232 | 291 | 78 | 103 | 159 | 132 | 37 | 67 | 204 |
日期 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
AQI | 270 | 78 | 40 | 51 | 135 | 229 | 270 | 265 | 409 | 429 | 151 |
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
AQI | 47 | 155 | 191 | 64 | 54 | 85 | 75 | 249 | 329 |
表2:2017年12月AQI指数表:单位(![]() )
)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
AQI | 91 | 187 | 79 | 28 | 44 | 49 | 27 | 41 | 56 | 43 | 28 |
日期 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
AQI | 28 | 49 | 94 | 62 | 40 | 46 | 48 | 55 | 44 | 74 | 62 |
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
AQI | 50 | 50 | 46 | 41 | 101 | 140 | 221 | 157 | 55 |
根据表中数据回答下列问题:
(Ⅰ)求出2017年12月的空气质量指数的极差;
(Ⅱ)根据《环境空气质量指数(AQI)技术规定(试行)》规定:当空气质量指数为0~50时,空气质量级别为一级.从2017年12月12日到12月16这五天中,随机抽取三天,空气质量级别为一级的天数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)你认为该市2017年初开始采取的这些大气污染治理措施是否有效?结合数据说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点与抛物线
的右顶点与抛物线![]() 的焦点重合,椭圆
的焦点重合,椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 且垂直于
且垂直于![]() 轴的直线截抛物线所得的弦长为.
轴的直线截抛物线所得的弦长为.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 恒过一定点.
恒过一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.8元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.

(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
(ⅰ)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
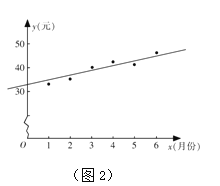
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校初三年级有![]() 名学生,随机抽查了
名学生,随机抽查了![]() 名学生,测试
名学生,测试![]() 分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
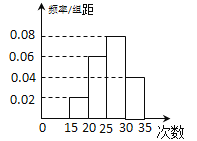
A. 该校初三年级学生![]() 分钟仰卧起坐的次数的中位数为
分钟仰卧起坐的次数的中位数为![]() 次
次
B. 该校初三年级学生![]() 分钟仰卧起坐的次数的众数为
分钟仰卧起坐的次数的众数为![]() 次
次
C. 该校初三年级学生![]() 分钟仰卧起坐的次数超过
分钟仰卧起坐的次数超过![]() 次的人数约有
次的人数约有![]() 人
人
D. 该校初三年级学生![]() 分钟仰卧起坐的次数少于
分钟仰卧起坐的次数少于![]() 次的人数约为
次的人数约为![]() 人.
人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次有600人参加的数学测试,其成绩的频数分布表如图所示,规定85分及其以上为优秀.
区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人数 | 36 | 114 | 244 | 156 | 50 |
(Ⅰ)现用分层抽样的方法从这600人中抽取20人进行成绩分析,求其中成绩为优秀的学生人数;
(Ⅱ)在(Ⅰ)中抽取的20名学生中,要随机选取2名学生参加活动,记“其中成绩为优秀的人数”为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)求平面![]() 和平面
和平面![]() 所成二面角(小于
所成二面角(小于![]() )的大小.
)的大小.
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com