
【题目】设函数![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)求整数![]() 的值,使函数
的值,使函数![]() 在区间
在区间![]() 上有零点.
上有零点.
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】一盒中装有除颜色外其余均相同的12个小球,从中随机取出1个球,取出红球的概率为![]() ,取出黑球的概率为
,取出黑球的概率为![]() ,取出白球的概率为
,取出白球的概率为![]() ,取出绿球的概率为
,取出绿球的概率为![]() .求:
.求:
(1)取出的1个球是红球或黑球的概率;
(2)取出的1个球是红球或黑球或白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点为
的两个焦点为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点![]() ,
,![]() 在椭圆上,
在椭圆上,![]() 在线段
在线段![]() 上,且
上,且![]() 的周长等于
的周长等于![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过圆![]() 上任意一点
上任意一点![]() 作椭圆
作椭圆![]() 的两条切线
的两条切线![]() 和
和![]() 与圆
与圆![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解游客对2015年“十一”小长假的旅游情况是否满意,某旅行社从年龄在![]() 内的游客中随机抽取了1000人,并且作出了各个年龄段的频率直方图(如图所示),同时对这1000人的旅游结果满意情况进行统计得到下表:
内的游客中随机抽取了1000人,并且作出了各个年龄段的频率直方图(如图所示),同时对这1000人的旅游结果满意情况进行统计得到下表:

(1)求统计表中![]() 和
和![]() 的值;
的值;
(2)从年龄在![]() 内且对旅游结果满意的游客中,采用分层抽样的方法抽取10人,再从抽取的10人
内且对旅游结果满意的游客中,采用分层抽样的方法抽取10人,再从抽取的10人
中随机抽取4人做进一步调查,记4人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设小明订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到,小明离家的时间在早上7:00—8:00之间,则他在离开家之前能拿到报纸的概率( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图.
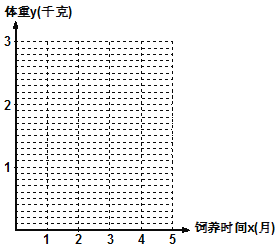
(2)请根据上表提供的数据,用最小二乘法求出变量![]() 关于变量
关于变量![]() 的线性回归直线方程
的线性回归直线方程![]() .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: 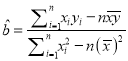 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”.给出下列命题:
①函数y=sinx具有“P(a)性质”;
②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f(2015)=1;
③若函数y=f(x)具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,则y=f(x)在(﹣2,﹣1)上单调递减,在(1,2)上单调递增;
④若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,函数y=f(x)是周期函数.
其中正确的是 (写出所有正确命题的编号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com